線形代数のまとめ　その３(行列式について)

線形代数

その２の続き

その２で写像って何だ？というとこから基底や逆行列についてメモした
最後で独立の意味って何だろう？とか任意のある行列に逆行列が存在するかの判定や任意でとった基底の組が基底としての条件を満たしているかの判断はどうすればいいんだろうという疑問が浮かんで終わった。続きをメモする。

ところで線形代数の授業を受けた人なら行列の他にも行列式というのを見たことがあるというか解かされたことがあるんじゃないだろうか

$$ \begin{bmatrix} 1 & 9 & 3 \\ 7 & 5 & 3 \\ 3 & 1 & 5 \end{bmatrix} $$

こんな形のやつ。自分は思考を停止して余因子展開したり2次の行列式なんかに関してはもう{ \displaystyle (ad-bc)}して終わりッッって感じに解いていた。

前回で行列は写像、基底の移り先を教えてくれるものという見方をした。2次元空間において基底の組{ \displaystyle ( \vec{e_1} , \vec{e_2} )}　(単位ベクトル { \displaystyle \vec{e_1} = (1,0)^{T} , \vec{e_2} = (0,1)^{T} })をとったとき
正方行列AとB
$$ A = \begin{pmatrix} 1.5 & 0 \\ 0 & 0.5 \end{pmatrix} B = \begin{pmatrix} 1 & -0.7 \\ -0.3 & 0.6 \end{pmatrix} $$
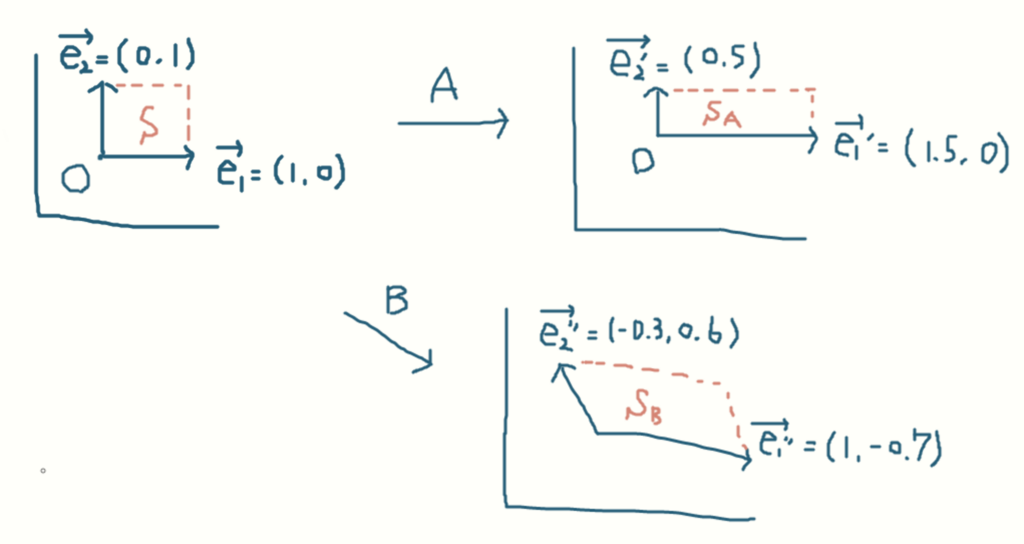
この2つの行列による写像はそれぞれ以下のようになる。
f:id:Owatank:20171223155552p:plain
元の基底ベクトルたちがそれぞれビヨーンと伸びたり縮んだり、方向自体変わったりした。

ここで線形空間ではベクトルの長さという概念はないが、この写像される前と後の基底ベクトルから成る四角形の面積を求めてみる。
ちなみに長さや角度の概念がある線形空間は内積空間と呼ぶそうだ

f:id:Owatank:20171223160036p:plain
上の画像のように、{ \displaystyle S}と{ \displaystyle S_A}、{ \displaystyle S_B}を求めたい。
{ \displaystyle S}を単位ベクトルからできる四角形の面積、横=1{ \displaystyle ( \vec{e_1})}、縦=1{ \displaystyle ( \vec{e_2})}として{ \displaystyle S = 1}とする。
{ \displaystyle S_A}は{ \displaystyle ( \vec{e_1})}が1.5倍、{ \displaystyle ( \vec{e_2})}が0.5倍拡大されたものだから、
{ \displaystyle S_A = \vec{e_1^{\prime}} \times \vec{e_2^{\prime}} = 1.5 \times 0.5 = 0.75 }となる。0.75倍ということは写像前より小さくなった。

{ \displaystyle S_B}は本には0.39倍と書いてあったがどうやって求めたんだ・・・・と悩んだが調べたら外積で求めることができるそうだ。電磁気学の授業でよく教授が右ねじ〜＾＾と言いながら親指をグルグルさせていたのをよく覚えている。

{ \displaystyle \vec{e_1^{\prime \prime}} = (1,-0.7)^{T} }と{ \displaystyle \vec{e_2^{\prime \prime}} = (-0.3,0.6)^{T} }が成す外積{ \displaystyle S_B}は
{ \displaystyle S_B = \vec{e_1^{\prime \prime}} \times \vec{e_2^{\prime \prime}} = 1 \ast 0.6 - (-0.7) \ast (-0.3) = 0.6 - 0.21 = 0.39 }
{ \displaystyle S_B}は 0.39倍とこっちも小さくなった。

ここで、

自分は思考を停止して余因子展開したり2次の行列式なんかに関してはもう{ \displaystyle (ad-bc)}して終わりッッって感じに解いていた。

この{ \displaystyle (ad-bc)}を見て欲しい。行列AとBが都合よく2次行列だしせっかくなので行列式とやらを求めてみる。2次行列の要素を
$$ \begin{pmatrix} a & b \\ c & d \end{pmatrix}$$
とする。このときAとBの行列式は
$$ detA = \begin{bmatrix} 1.5 & 0 \\ 0 & 0.5 \end{bmatrix} = 1.5 \ast 0.5 - 0 \ast 0 = 0.75 $$
$$ detB = \begin{bmatrix} 1 & -0.7 \\ -0.3 & 0.6 \end{bmatrix} = 1 \ast 0.6 - (-0.7) \ast (-0.3) = 0.39 $$

!?

各行列式の値 detA、detBと面積の値{ \displaystyle S_A}と{ \displaystyle S_B}が一致している・・・しかもBの行列式は心なしか外積と計算式が似ている・・・・・・・・

というわけでこの本では上で求めた面積の拡大率のことを行列式とよぶ。(3次なら体積拡大率とも言える)
授業や試験に出た2次の行列式の問題はつまり四角形の面積の拡大率を計算させられていたということか・・・
イケてる小学生は行列式で平行四辺形の面積を求めるのかもしれん

ちなみに行列式は正方行列に対してだけ定義されるものなため正方行列じゃないものに関しては行列式は考えないそうだ

行列式は行列の要素によっては計算結果から負の値が出ることも考えられる。負の面積拡大率って何だろう？という問いに関しては面積を求めたい図形が裏返しになる、イメージだそうだ。外積では「向き」という考えがあったしそんな感じかな。

f:id:Owatank:20171223165307p:plain

写像する前の画像(平面)は写像した後だと反転している(ステッキとか)。「面積自体は拡大したけど写像していた向きと同じ向きに拡大されたわけではない」ということを示したい時とかだと負の値を見れば一発でわかるね便利だね

行列式には以下のような性質がある
* { \displaystyle detI = 1}
* { \displaystyle detAB = det(A)det(B) }

一つ目は単位行列{ \displaystyle I }が「写像しても何も変化しない」行列なので、つまり元の面積を1倍すると考えると納得できる。
二つ目は行列Bで拡大して次に行列Aで拡大した拡大率{ \displaystyle det(AB)}は{ \displaystyle detB}倍して{ \displaystyle detA}倍したと同じということ。

行列式が面積拡大率ということなら行列式が０になるというのは何を意味するだろう？面積が0倍・・・？
上にある単位ベクトルが基底のときの行列式({ \displaystyle S})は１だった。これを何かしらの行列で写像して、その結果の拡大率が０ということは元々あった面積がぺちゃんこになってしまったということ

f:id:Owatank:20171223170701p:plain

こんな感じだ。元々の面積というよりは基底ベクトルからできていた平面がほぼ点にしか見えないような平面へと写像されるイメージ
またはこんな風に写像されてしまったかもしれない
f:id:Owatank:20171223171035p:plain
面積が０ということは平面が作れないということ。写像した後の基底ベクトルが同じ向きを向いてしまったら、平面は作ることができない。

そんなこんなで(2次元空間において)行列式が二つの基底ベクトルが成す面積拡大率を表すもので、行列式の計算結果が０になってしまうことはその時の基底ベクトルが同じ向きを向いているか、1本しかない、などの状況が考えられる。

こんな状況になる基底は基底としての条件を満たさないということだった。

f:id:Owatank:20171219121642p:plain

上の画像のようになってしまう基底ベクトルでは基底は作れなかった。つまり

行列式を求めることで移された基底の組が基底の条件を満たすかどうかの判定ができる！！！！！

行列式スゲー

次に{ \displaystyle detAB = det(A)det(B) }の性質を使って{ \displaystyle det(AA^{-1}) = det(A)det(A^{-1}) }がどうなるか考える。
逆行列の定義から{ \displaystyle AA^{-1} = I }となるので、左辺は{ \displaystyle det(AA^{-1}) = det(I) = 1 }となるはず。
そうなると右辺も１にならないといけない。{ \displaystyle detA^{-1} }が{ \displaystyle detA }の値の逆数であれば両辺は成立する。

{ \displaystyle det(A^{-1}) = \frac{1}{det(A)} }という関係式が得られる。

このとき面積拡大率が０、{ \displaystyle detA }が０の時この関係式が成り立たないことがわかる。
成り立たないってことは { \displaystyle A^{-1} }が存在しないって言ってもおかしくない。

ん？

ちょっと待てよ・・・ということは

行列式を求めることでその行列に逆行列が存在するかどうかも判定できる！！！

行列式スゲー！！！！！！！！！！

また逆行列が存在するかを行列式から求めることができる→行列式は正方行列にしか定義されない→逆行列は正方行列でなければ存在しないという前回の単射・全射あたりがより納得できる

まとめると、n次正方行列Aがあって{ \displaystyle detA = 0}のとき * そのときのn本の基底ベクトルから成る基底の組は、いずれかのベクトルが他のベクトルで表現できるような独立でない、またはn本より少ない状態にある。 * 逆行列が存在しない

ということがわかった。

逆に{ \displaystyle detA = 0}じゃないなら、そのn次正方行列Aは正則行列ということが言えるのがわかった。

n次のときで証明してない？買おう

長くなったので余因子展開とか別の行列式の性質はまた今度

そういえば外積の求め方と行列式の計算方法は何か関係があるんだろうか？どっちから派生したとかかな