一次元と和解を試みる 多分その1
お久しぶりです。1ヶ月に1回は更新するつもりが一回ダレるとなかなかどうして熱量が湧いてこない。ちまちまメモという名の下書きでも残しておくべきかなあ
今まで自分がキカイガクシュウで遊んでいたのは入力が画像のみのものばかりだった。とはいえ世の中には言語や音声、3Dモデルとか画像だけじゃないものもどうこうしようと研究されている訳で。2次元は俺の嫁という格言があるが視野を広げるためにも心機一転だ一次元と和解してみよう
ここで指している一次元は音声とかの波形としていいですか?
深く考えず波形を作ってみよう。よいしょ

中学の頃から目にするsin波を作ってみた。波形を作る際1秒間に何個信号をサンプリングするかを決めなくちゃいけなくて、CDだと1秒に44100回も信号をサンプリングするんだけどお遊びなので1秒に12000個の信号をサンプリングした。
もう一つ大事な要素に音の高さ(図で言ううねうねの回数)があるがその周波数の決め方としては以下の音階の周波数を参考にした (261.626 ~ 493.883 Hzのとこ)
https://tomari.org/main/java/oto.html
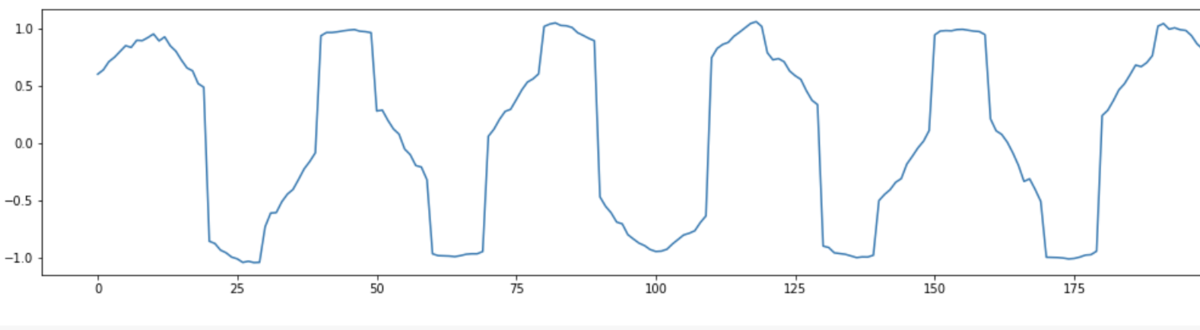
上の図はミの音(329.628Hz)の周波数のsin波をプロットしたが、シの音(493.883 Hz)だと次のような波形になった

うねうねが増えている、増えていると言うことはビャーな感じ。つまり音が高いのだ。絶対音感がなかったとしてもプロットすればどっちのが音が高いのか一目でわかるのだ...
作ったのはいいけど何して遊ぼうかな。あえてノイズを加えて、そこから入力を元通りに復元することを考えてみようかな
ノイズってどう加えればいいんだ、この波形がちょっとギザギザすればノイズっぽいイメージが直感だとあるんだけど。元の信号の値を [-ε,ε] の範囲でシフトさせればできるだろうか?デノイジングはノイズの確率分布を推定するっていうしね、入力波形と同じ長さ(行列サイズ)で正規分布から値を持ってくる。それに重み 0.05 をかけて入力波形に足し合わせる。(掛けないと元の入力の形状がわからないくらいの波形になっちゃった)
noise_map = 0.05*np.random.normal(size=X_wav.shape)
X_noise = X_wav + noise_map
ノイズ自体の波形と足し合わせた結果の一部をプロット(入力波形はミの音 )


音としてはちゃんとミの音を保ちつつ後ろでサーと砂音がなっている感じだった。これでひとまず良さそう
次に考えるのは、このノイズが含まれた波形だけを与えられたときに ノイズの分布の抽出 or オリジナルのミの音の波形の復元ができるかということ。よくある y = Ax な形?違うか
自分で考えておいてなんだけどすごく悩む。イメージとしてはこのちょっとデコボコした部分をスムージングすれば元の入力波形が復元できそうなんだけど
そうだ。このノイズありの波形は元の入力波形をこうしたものと見ることはできないか!?
よくある平均が0で分散が1に直す正規化のやつ。Yがノイズありの方だとしたら、この Y に標準偏差を掛けて平均を足してやれば X が得られそうじゃないか
N個の信号をK個 (<N) ずつ区切ってその連続したK個の信号に対して平均と標準偏差を求めこの操作を行なってみる
X_noise_tmp = X_noise.copy() K= 10 for i in range(0,len(X_noise_tmp), K): local_wav= X_noise_tmp[i:i+K] local_wav_mean = np.mean(local_wav) local_wav_std = np.std(local_wav) X_noise_tmp[i:i+K] = (X_noise_tmp[i:i+K] * local_wav_std) + local_wav_mean
操作から得られた波形
君なんか写真と違くない?音声として聞いたところノイズの砂音は聞こえなかったが元の入力波形よりどこか音が高かった気がした。
これじゃ駄目だ。波形といえばフーリエ変換、フーリエといえばいつぞやの冬に読んだフーリエの冒険から野菜ジュースの例を思い出す。
せや、野菜ジュースをトマトや人参といった成分に分解して見るように、この波形も音の高さや波形としての滑らかさとか何かに分解しよ。行列だって同値分解や特異値分解、シュア分解とかたくさんあるしな分解大事
高校生の時のsinや のマクローリン展開とかモーメント母関数ってやつとかの多項式での表現というか、きっとできるはず。だってこれ一応ベースがsin波だし...
そのためにフーリエ変換するぞ!!!ヤコビ法?いや知らないです...
フーリエ変換って特定の波形をsin波とcos波のいくつかの足し合わせで表現できるって考えを元に変換するはず。線形代数勉強したら正弦波がある波形の基底を成しているとも受け取れるような。多項式での表現といっても有限個の多項式での表現しないといけないから N = 256 と決めうちしてフーリエ変換を試みる
N = 256 X_tmp = X_wav.copy() FFT_orig_wav = np.zeros(X_wav.shape) + 0j for t in range(len(FFT_orig_wav)): p = 0. for x in range(N): p += X_tmp[x]*np.exp(-2j*np.pi*t*x/N) FFT_orig_wav[t] = p X_noise_tmp = X_noise.copy() FFT_noise_wav = np.zeros(X_noise_tmp.shape) + 0j for t in range(len(FFT_noise_wav)): p = 0. for x in range(N): p += X_noise_tmp[x]*np.exp(-2j*np.pi*t*x/N) FFT_noise_wav[t] = p
オリジナルの入力波形とノイズ込みの波形をプロットする(1000個の点まで)

ノイズの波形(オレンジ)が低いところでビヨビヨしている。ここがオリジナルとの決定的な違いじゃないか?!
N=256と決めうちしたからか変換した波形もどこか0から256点の信号の区間で周期があるように見える。RGB空間をHSV空間に写すそんな感じでフーリエ変換した先の軸が異なるから元の横の時間軸を適切な角周波数の軸に直す(時刻tの軸をsinθのθを軸にする)
x_scale = np.linspace(0,12000/2,N) plt.figure(figsize=[18,4]) plt.plot(x_scale,FFT_orig_wav[:N],'-',ms=1,label='orig') plt.plot(x_scale,FFT_noise_wav[:N],'-',ms=1,label='noise') plt.legend()

あってんのかなこれ。絶対違うなあとで修正する
フーリエ逆変換を用いれば変換する前の波形に戻せるので、こっちのフーリエな空間で波形を少しいじって逆変換してやれば、変換する前の波形を対応していじった時の波形が得られるはず。
どうも縦軸[-2,2]あたりで微小に振動しているこのグニョグニョを水平線を伸ばすように適当な値 x といった固定値で大人しくさせれば良さそうな気がする。固定値の x はこの振動している区間の平均をとったものにして、次のようなフィルターをかけてみる
FFT_noise_wav_tmp = FFT_noise_wav.copy() constant_x = np.mean(FFT_noise_wav_tmp[10:240]) for i in range(len(FFT_noise_wav_tmp)): if(FFT_noise_wav[i]< -2 or FFT_noise_wav[i] < 2): FFT_noise_wav_tmp[i] = constant_x
フィルターをかけたら次のようになった

完璧とはいかないけれど、これはもう勝っただろ
逆フーリエ変換をかけて元に戻してみるぜ!!!!!!!!!!!
N = 256 fft_noise_tmp = FFT_noise_wav_tmp.copy() IFFT_noise_wav = np.zeros(fft_noise_tmp.shape) + 0j for t in range(len(IFFT_noise_wav)): p = 0. for x in range(N): p += fft_noise_tmp[x]*np.exp(2j*np.pi*t*x/N) IFFT_noise_wav[t] = p IFFT_noise_wav = IFFT_noise_wav/N

ほぼオリジナルと似ている。もう成功でいいや
ノイズありの波形に復元した波形を引くとちゃんとノイズ自体の波形も得られた。
やっていることは音声のデノイジングだったけど、よくよく考えるとラジオはどうやってデノイジングしているんだろう?だってあれ計算機ではないじゃん?フーリエ変換って回路組んでできるのかなあ、授業で抵抗やT2ファージみたいなコンダクタとか使ってハイパスフィルターの実験した記憶あるけど、それを通してから音声を出力してるのかな。すみません、ファインマンさん・・・(考えるだけでラジオを直す少年を読んだ)
他にも遊ぶネタはあるんだけど疲れたのでここまで
遊びで使ったコード