WGANの論文読んでTensorflowで実装する その1
前回、間違えてUnrolledGANの論文を読んでしまった。
このWGANというのが本当は読もうと思った論文。正直UnrolledGANを先に読んでなかったらWGANの理解が深まらなかったと思う。読んでてよかった
という訳で論文はここからどうぞ
あとコードも先に置いておく
WGANという名前が付いてるから、このWが重要になってくる。WはWassersteinの略。わずさーなのかわっさーなのか英語がカスなので読み方がわからん・・・
Wassersteinというのは論文ではEarth Mover (EM) distanceとも呼ばれる。distanceだから距離を表すもの。この距離をGANに使ったらいい感じになったってことなのか?と読み始めに思った。
今まで自分が読んだGANはどれも GeneratorとDiscriminatorの学習速度のバランスが悪いから何とかする、というのだった。両モデルにバッチ正規化層を追加したり、学習方法を変更したりとか、、
WGANはざっくりいうと、バランスを調整するためのバッチ正規化といったトリックを使う必要がなく、単なるMLPを用いたGANでもEarth Mover (EM) distanceを使うことで学習が崩壊せずに上手く行くぜってことが書いてある。
ス、スゲー!!!わずか論文3ページ目でこのインパクト・・・。続きが知りたくなるやんけ
それで何でEarth Mover (EM) distanceが出てくるんだよってなる。ここで生成モデリングについて考える。
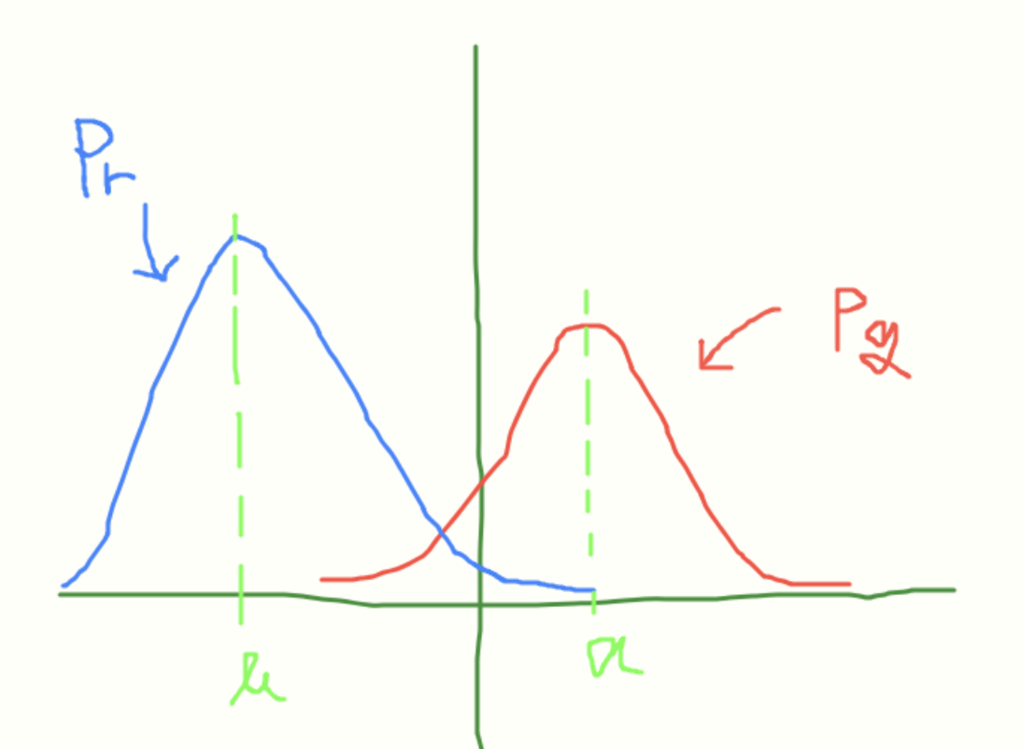
を「知りたい目的のデータの分布」とする。
今をこの
に近づける、もとい形状が似るようにしたい。どうするか・・・
がパラメータ
で作られているとしたら、
の値を変えてやれば形状が変わったり、軸
も別のところに移動できるはず
じゃあパラメータの値を上げたり下げたりするとして、どっちの操作をすればいいのか。パラメータが3つの値から成ってたら、一つ目の値は今より小さくして、二つ目の値は今より大きくして、、という決定をどうすればいいかわからない。
今パラメータが持つ値を全て今より大きくしたとき、
は
に近づいているのか、遠のいているのか、その情報が得られれば、「パラメータを大きくしたら
に遠のいたから下げよう」といったことができそうだ
近いってどう数値として表すか・・・シンプルだと
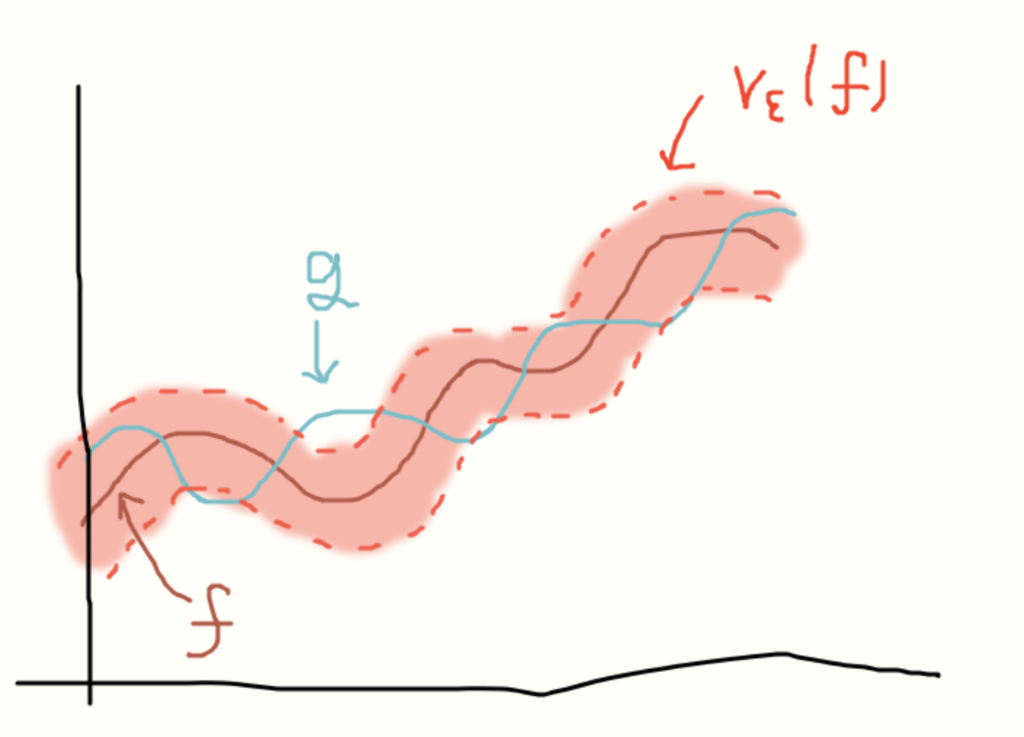
関数 と関数
の二つがあったとして、この二つが近いとしたら
がとる値の±
した範囲(赤の部分
、
は小さい正の数)に関数
のとる値が入っていれば、
が小さい値であるほど赤の範囲は狭くなるからより二つの関数が「近い」といえるはず。
| |みたいに距離を使えば二つの分布が似ているかどうかがわかりそうだ(∩^ω^∩)
だから EM距離を使うぜ といった話になるんだな。多分・・・
話は戻って、論文では EM距離がすごいんだぜーというのを説明するためにEM距離含めて分布が近いかどうかを教えてくれる距離を4つ紹介している
せっかくなので一つずつ見ていく
まず前提として をコンパクトな集合とする。有界な閉集合ならコンパクトだけど、コンパクトは後なんか被覆が云々で言えたような・・・
論文だと 例として [0,1] の閉区間とかーって書いてある。うん、、
を
上での確率測度(probability measure)とする。
が確率測度といえるための条件満たしてるぜってことでいいかな
1. Total Variation (TV) distance
を
でのボレル集合とする、と書いてある。 え何それは・・・
話を聞いたら、 という集合の中で、
でその値を知りたいもの全部を含めた集合ってことでいいらしい。
その認識で考えれば、絶対値の差をとってるし、sup(上限)を選べってあるから
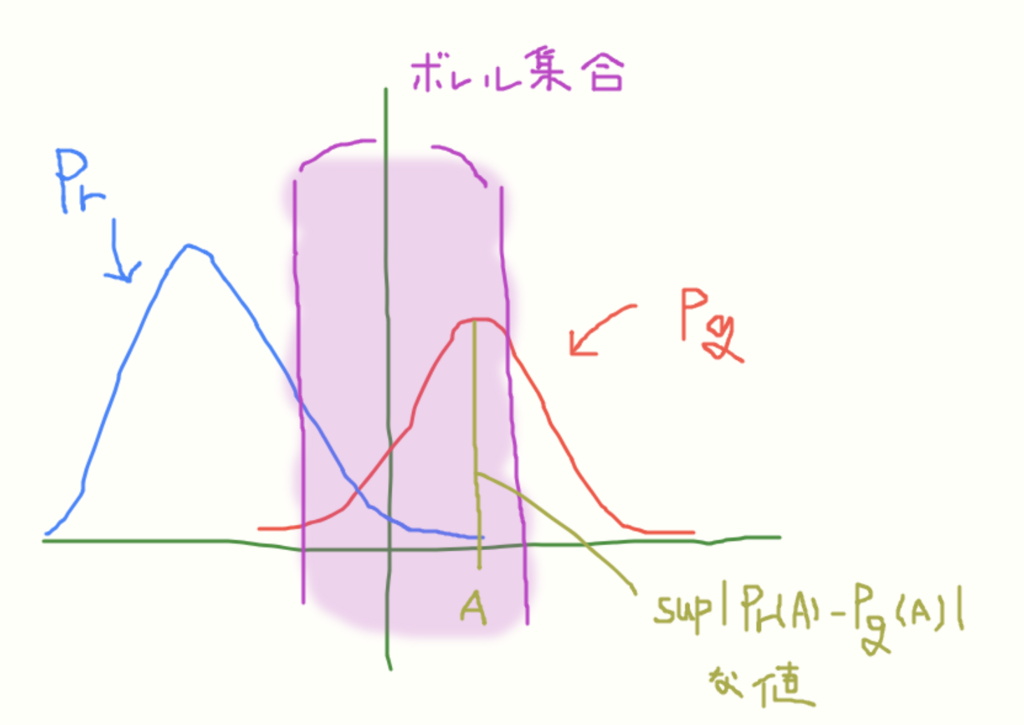
こんな感じかな。(図ではボレル集合を一つの範囲でしか取らなかったけど)
確率の値での差を取るから、もし二つの分布が一致してたらTV距離は最大で0、一致してなかったら最大で1を取るから、 この距離は小さい方が近いってことを表してくれるのか。
2. The Kullback-Leibler (KL) divergence
KLダイバージェンスについては解説の記事が沢山あるから省くけど、と
が似てると、logの部分は log1 になってく、つまり 0に近づいていくので距離としては値が小さいほど二つが似ていることになる。分母の
が 0 をとったらその・・・計算できないというか・・possibly infiniteと書いてあった。
ダイバージェンスという単語は電話レンジが云々のアニメで知ってた。
でも「距離」の紹介なのに「ダイバージェンス」っておかしくね?って思うんですが、距離 は
この3つの条件を満たしていればを距離と(正確には
をxとyの距離)いえる世の中のルールらしい
ダイバージェンスは二つ目を満たしてないから距離とは言えないとか
ところで距離の公理を初めて知った時、三角不等式が点列の収束を調べるときに使うものと知ったんですが、高校時代ナニコレ?と思ってたものがすげー役割を持ってたって思うと興奮した
3. Jensen-Shannon (JS) divergence
ジェンセ・・イェンセン・・論文でも他3つの距離と比べて説明少ないんだけど、の分母が2になってるから無限大になるのは回避できそう?
4. Earth-Mover (EM) distance or Wassterstein-1
これが今回の主役のEM距離だけど、式がむずそう
まず、 は同時分布
の集合を表すそうだ
論文ではどうやらtranspoted、日本語だと輸送がうんぬんと言っている。これも話を聞いてみたら

二つの分布をそれぞれ四角のブロックの集まりで表す。
がもつブロックを、
の方に移すとする。
と重なっていないブロックを移していけば、いつかは
と同じ形になる
ここで移し方には、初期の分布の設定にもよるけど、沢山のパターンがあると思う。
ブロックを移すにも時間がかかる。EM距離は求めたい時の分布の位置状態で、ブロックの移す時間が一番少ない、最小コストの値を二つの分布の「近さ」として与えてくれる。
の右端にあるブロックを
の左端の方に移したら、移すのにめっちゃ時間がかかってもったいない。
つまりブロックの輸送を開始する時点で、二つの分布が似ていれば、もともとブロックの移すコストも少なくなるはずだろってことか。発想がすげえ・・・
地味にこのEM距離はコンパクトな集合においてだけ使えるといったものじゃなくて、コンパクトじゃない集合においても使えるらしい。その時不思議な結果が出るとか何とか・・・
論文ではこの4つの距離を紹介したあと、この4つの距離を使ってシンプルな ([0,1]の一様分布 )を
で近づけていく実験をしてた。
結果としては EM距離は以外は、二つの分布がぴったり重なる時と重ならない時で値が TV距離だと 1と0、 JSダイバージェンスだとlog2と0、といったように極端な結果を出していた。
論文の実験図だとこんなん
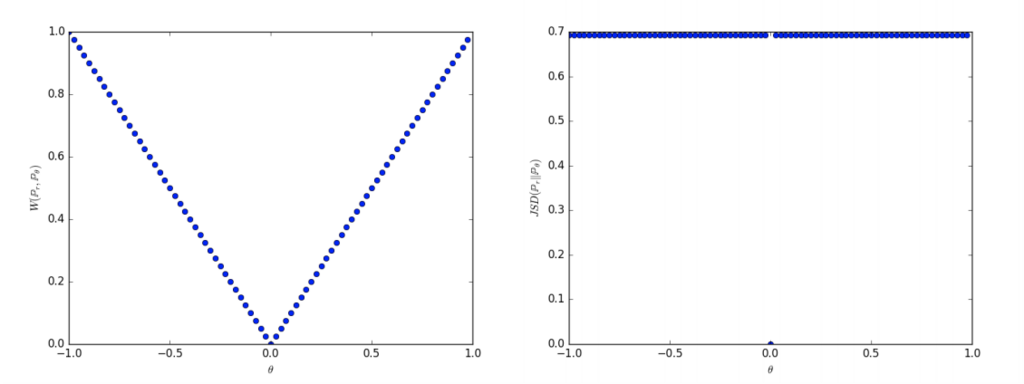
左がEM距離の値、右がJSダイバージェンスの値
のパラメータ
を0に近づけていくのがゴールで、EM距離はパラメータ
が0に近づいていくほど、徐々に小さくなっていくのに対して、右のJSダイバージェンスでは、
=0以外では
の値を取り続ける。
よくスイカ割りするじゃないですか。目隠しして歩いてスイカにたどり着くとして、1歩歩くごとにその地点からゴールまでの距離を教えてくれる人が
「ゴール以外は全部と教えてくれる人」と、「ゴールからあと
メートル(ゴールに近くほどKが小さい)と教えてくれる人」だったらどっちのが嬉しいっていったら自分は後者。スイカ割りしたことないけど
きっと生成モデリングにおいても、がある「距離」が小さくなる方向に収束していくにつれて、
から作られる
が目的の分布
に近づいていけるなら、それが嬉しいパラメータの修正の仕方なんだろう
だからEM距離はすごいんだぜー というのがわかったけど、どうやら上のEM距離の定義式のまんまGANの目的関数として使うのは厳しいらしい。ええ・・・
長くなったので分ける
この論文読む前に志賀浩二先生の「位相への30講」を読んでいなかったらほぼ即死だった・・・
でもこの論文で「測度」の公理なり、ちょいちょい見ていた「加法族」の意味なり知ることができてよかった(∩^ω^∩)
測度論はフーリエか何かの勉強で「オイラーの公式が成り立つことを詳しく知るには「測度論」について調べることをオススメする」みたいな文章があって単語だけ覚えてたんだけど、こんなとこで会うとは思わなんだ・・・
ちょいちょい意味が繋がるのは嬉しい