GANの論文を読んだ自分なりの理解とTensorflowでのGANの実装メモ

タイトルのまんま

VAEの理解のために変分ベイズの方を優先したいが卒業がかかっているので先にGANの論文を読んだ
GANの論文って多いっぽいが以下のリンクのものを読み読みした

[1406.2661] Generative Adversarial Networks

これは自分の頭がお猿さんなせいもあると思うがハチャメチャ読みやすかった
Algorithm 1というパートのところは感動で涙が出た。な、なんてわかりやすい解説なんだ・・・・・

GAN(Generative Adversarial Nets)よろしく敵対学習は今自分が知りたいVAEと同じく生成モデリングのひとつ。VAEの論文を読んだときにもあったが既存の生成モデリングの手法は、MCMCといった計算時間がかなり掛かるものが依存関係として必要だったり、そもそも観測データの周辺分布の計算の積分が計算困難なことがあったりして困っていたっぽい(近似も困難だとか)
このGANはそういった計算の困難なところとかを回避した生成モデリングの手法。この手法ではモデルの学習中にMCMCが必要ないと書いてある。マジで？

そもなんでGenerative Adversarial Netsといった強そうな名前が付いたのか。論文での例を使うことにする。

本物に近い偽札を作りたい人がいたとする。偽札を作るモデルを生成モデル G (Generate)とする。
f:id:Owatank:20180417172250p:plain

その一方で、偽札の検出をしたい人がいる。本物か偽札かどうかを見分けるモデルを識別モデル D (Discriminative)とする

f:id:Owatank:20180417172641p:plain

GANではこの2つのモデルを同時に学習させて、生成モデルの作った偽札が識別モデルによる本物との識別が難しいくらいのものを作れるようにしていく。
偽札の例だと2つのモデルは作るものと見分けるもので反対のもの同士だからここら辺から敵対という名前が付いたといったことが書かれていた、、はず、、

どう学習するかというと生成モデルが本物と同じくらいの偽札を作るように、識別モデルが受け取った入力が本物か偽物か完璧に識別できるようにする、ある目的関数を設けてそれを最適化していく。具体的には確率勾配法を用いて最適化していく。

生成モデルと識別モデルの両方を多層パーセプトロンで構築すると、逆伝搬とドロップアウト、順伝搬から生成モデルによって得たサンプルの3つの要素を使うことでよりシンプルにそして同時に両モデルの学習が可能となると書いてある。天才か・・・

多層パーセプトロンを用いるのはわかったけどどういった枠組みなんじゃい。

生成モデル G は事前入力ノイズ変数 { \displaystyle P_{\boldsymbol{z}} (\boldsymbol{z}) } とパラメータ { \displaystyle \theta_g} をもつ。そして { \displaystyle G(\boldsymbol{z} ; \theta_g) }はデータ空間へのマッピングを表すと書いてあったが要は入力変数zと生成モデル自身が持つパラメータ { \displaystyle \theta_g} を使って目的のデータと似たデータを作るってことかな。生成モデル G が多層パーセプトロンによって表され、微分可能な関数となっている。このGが観測データ{ \displaystyle \boldsymbol{x} } (上の例で言えば本物のお札) に対するジェネレータの分布{ \displaystyle p_g }を推定するために必要なのだ。

2つめの多層パーセプトロンとして { \displaystyle D(\boldsymbol{x} ; \theta_d) } を定義する。これは入力ベクトル { \displaystyle \boldsymbol{x} } と識別モデル自身が持つパラメータ { \displaystyle \theta_d } を用いて識別結果(偽物か本物か)を単一のスカラーを出力として返す。
関数 { \displaystyle D(\boldsymbol{x}) }は入力{ \displaystyle \boldsymbol{x} }がジェネレータの分布{ \displaystyle p_g }から来ているのか、学習に用いているデータの分布から来ているのかを確率として表して、出力として返す。二値分類みたいなものの解釈でいいだろうか

識別モデル D は訓練データ(本物のお札データ)と生成モデル G からのサンプルの両データに対して正しいラベル(1は本物、0は偽物といったラベル)を割り当てる確率を最大にするように学習する。

そして生成モデル G は次の式が最小になるように学習する

{ \displaystyle log(1-D(G(\boldsymbol{z})) ) }

偽札のラベルを 0 とすれば、上の式は log(1-0) で 0 が最小の値になるから、{ \displaystyle G(\boldsymbol{z}) }が作った偽物を{ \displaystyle D(G(\boldsymbol{z})) }がしっかり偽物と識別するように学習させろよってことだな

GとDを同時に学習させるのでこれらをまとめた値関数{ \displaystyle V(D,G) }を考えていく

{ \displaystyle \min_{G}\max_{D} V(D,G) = \mathbb{E}_{\boldsymbol{x} \sim p_{data(\boldsymbol{x})}} \ {[}logD(\boldsymbol{x}){]} + \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}(\boldsymbol{z})}} \ {[}log(1-D(G(\boldsymbol{z}))){]} }

数式書くのクッソ疲れた。右辺の第1項は{ \displaystyle logD(\boldsymbol{x}) }だから本物のお札を入力として渡している。期待する値は{ \displaystyle logD(\boldsymbol{x}) }が最大になればいいのだから log(1) = 0 でその平均、期待値は０が望ましくて、第2項は上で述べたように { \displaystyle D(G(\boldsymbol{z})) = 0} が望ましい値であり結果としてその周りの期待値も 0 に近い方が良いで合ってるだろうか

お猿に優しい学習アルゴリズムの教育的な説明が書いてあった。次のように自分なりに理解した。
訓練データのサンプルから作られるデータ分布{ \displaystyle p_x } 、生成モデルGから作られるジェネレータ分布{ \displaystyle p_g } 、入力が本物か生成モデルから作られたものかを確率的に表す識別モデルDの3つが画像のようになっているとする。

f:id:Owatank:20180418103634p:plain

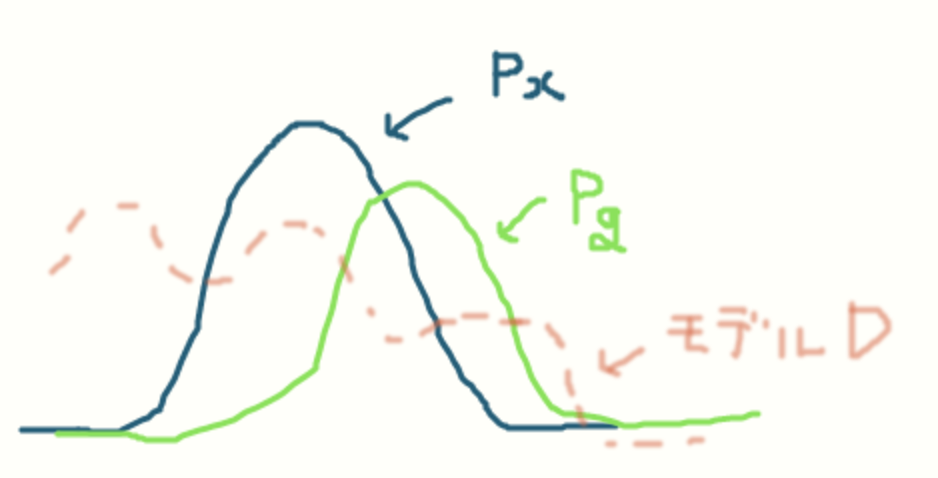
生成モデルGが本物に近いものを生成できるようにするということは上の図のデータ分布{ \displaystyle p_x }の形状とジェネレータ分布{ \displaystyle p_g }の形状が一致、もしくは限りなく近くなればいいのがわかる。そうするには上記の{ \displaystyle V(D,G) }を最適化しろと論文が述べている。

過適合の問題を避けるために、先に識別モデルDの更新を kステップ 行ってから、生成モデルGを更新後の識別モデルDを元に 1ステップ 更新すると書いてある。
Dはデータからサンプルを識別するように学習していく。具体的には次のように学習する。

{ \displaystyle D^{\ast}(\boldsymbol{x}) = \frac{p_{data}(\boldsymbol{x})}{p_{data}(\boldsymbol{x})+p_{g}(\boldsymbol{x})} }

生成モデルGの更新が終わった後にまた識別モデルDの更新を行うが、そのときのDの勾配は入力が本物のデータとして分類されるような可能性が高い方に生成モデル{ \displaystyle G(\boldsymbol{z}) }を導くと書いてある。

識別モデルDを学習する(kステップ)
G の持つ事前入力ノイズ変数{ \displaystyle P_g(\boldsymbol{z}) }からm個のノイズをサンプリングする。これら{ { \displaystyle {\boldsymbol{z}}^{(1)} , ... , {\boldsymbol{z}}^{(m)}} }を元にm個の偽物を生成する。そして訓練データセット(データ分布)からm個の本物をサンプリングする。2つから次のようにDを確率勾配法を用いて更新する。

{ \displaystyle \nabla_{\theta_{d}} \frac{1}{m} \sum_{i=1}^{m} {[}logD({\boldsymbol{x}}^{(i)}) + log(1-D(G({\boldsymbol{z}}^{(i)}))) {]}}

f:id:Owatank:20180418105655p:plain
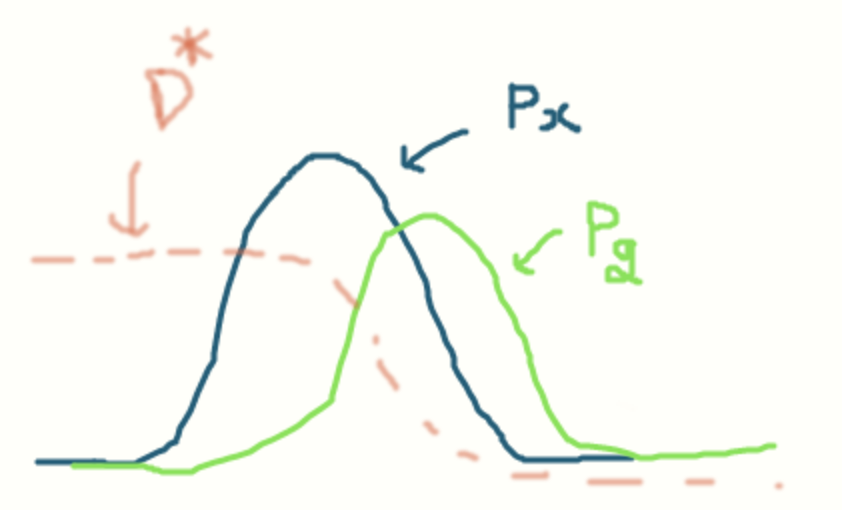
{ \displaystyle p_x }と{ \displaystyle p_g }が似ているところは識別が難しい=値が大きい(はっきりしている)ということ。真ん中あたりは形状が違うから値があやふやになっている感じ・・・なのか・・・？エントロピーみたいなもん？

このD(の勾配)を元に{ \displaystyle G(\boldsymbol{z}) }がデータ分布と類似するように学習させる。
上と同様にG の持つ事前入力ノイズ変数{ \displaystyle P_g(\boldsymbol{z}) }からm個のノイズをサンプリングする。これら{ { \displaystyle {\boldsymbol{z}}^{(1)} , ... , {\boldsymbol{z}}^{(m)}} }を元にm個の偽物を生成する。そしてその偽物たちから次のようにモデルGを確率勾配法より更新する。

{ \displaystyle \nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m} log(1-D(G({\boldsymbol{z}}^{(i)}))) }

f:id:Owatank:20180418110144p:plain

これで１エポックが終了か？これを何エポックか繰り返していくと
f:id:Owatank:20180418111411p:plain

{ \displaystyle p_x }={ \displaystyle p_g }となるくらいに類似することが可能なはず。このとき{ \displaystyle D(\boldsymbol{x})}は2つが似すぎていて入力がどちらのものか判断が難しい={ \displaystyle \frac{1}{2} }の値をとるということなんだな

2つの確率密度分布{ \displaystyle p_x }と{ \displaystyle p_g }が類似していることを確かめる指標としてカルバックライブラダイバージェンスは使えないんだろうか？と思ったが、その後のアルゴリズムがちゃんと機能するかの裏付け？っぽい Theorem のパートで出てきていた。うーん証明難しい

損失関数の定義からアカン・・・めっちゃ自分でも作れそうなほどシンプルやんけ・・・と思ったのでTensorflowで実装してみた
ソースはここ

github.com

GeneratorとDiscrimitorの作成において、論文通りMLPで構築した。
ノイズ事前分布については正規分布のがいいのかと思ったが一様分布を用いている人が多かったのでそっちにした。
最適化の方法は Adam でいいかと思ったけど論文通りに Momentum で行った方が割とうまく行ったので論文のモデル設定に従った。

最初に損失関数を次のように定義していた

self.dis_loss_X = tf.log(self.discrimitor.run(self.input_X))
self.dis_loss_G = tf.log(self.label_t1 - self.discrimitor.run(self.generator.run(self.gen_z,self.is_train)))
self.dis_loss = -tf.reduce_mean(self.dis_loss_X + self.dis_loss_G) + dis_norm_term*dis_lambda_
self.gen_loss = tf.reduce_mean(tf.log(self.discrimitor.run(self.generator.run(self.gen_z,self.is_train))))

識別モデルの方は上で定義していた通りに実装したが、生成モデルは 1 - D(G(z)) じゃないやんと思うが、論文において

{ \displaystyle log(D(G({\boldsymbol{z}}^{(i)}))) }


こっちのが収束がいいとか云々が少し書いてあった。
生成モデルで 1 - D(G(z)) を最小にするというのは生成したものが偽物とわかるようにパラメータを更新してねということになるから D(G(z)) のがいいよな・・・でもなぜかこれを最大化しろと書いてあって困ったがいう通りに従って-tf.reduce_mean()ではなくマイナスを取り去ったtf.reduce_mean()にした

そんなこんなでこれで学習を行ったところ損失がnanやinfになったりしてダメだった。そのせいか生成した画像は真っ暗なものしかできなかった。

損失関数は結局次の形で落ち着いた(後ろのnorm_termは重み減衰)

self.dis_entropy_X = tf.nn.sigmoid_cross_entropy_with_logits(labels=self.label_t1, logits=input_X)  
self.dis_entropy_G = tf.nn.sigmoid_cross_entropy_with_logits(labels=self.label_t0, logits=generated_X)   
self.dis_loss = tf.reduce_mean(self.dis_entropy_X + self.dis_entropy_G) + dis_norm_term*dis_lambda_
        
self.gen_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=self.label_t,logits=generated_X)
self.gen_loss = tf.reduce_mean(self.gen_entropy) + gen_norm_term*gen_lambda_

クロスエントロピーを使った。生成モデルに関しては、正解ラベルを本物 = 1 のラベルを与える。
こうすることで識別モデルでは生成モデルのものを偽物と判断するように学習していって、生成モデルは識別モデルを騙せるくらいの本物に近いものを作れるように学習していけるのだ・・・

次に詰まったのは最適化を行う際のパラメータの指定だった
最初はminimizeの部分でvar_listの指定をしていなかった。しかしこれを指定しないと、生成モデルの最適化を行う際に生成モデルのパラメータの更新と一緒に識別モデルのパラメータを偽物を本物と識別するような誤った方向に更新してしまう。

参考にしたもの
TensorFlowで特定の変数を指定して学習させる方法
TensorFlowで必要な変数を選択してsave/restoreする

ようは識別モデルの更新には(生成モデルの推論結果を更新に用いるが)識別モデルのパラメータのみを、生成モデルの更新には(識別モデルの推論結果を更新に用いるが)生成モデルのパラメータのみを更新するようにしないと学習がうまくいかない(´･ω･)

両モデルのMLP構築におけるパラメータのユニット数や初期値にも苦労して何とか次のような結果が得られた
f:id:Owatank:20180420165454p:plain

これはMNISTのデータセットの中の手書き数字が 4 のみのデータで学習したもの
はっきりした形のものは得られなかったが、それっぽい形状が得られてるんじゃなかろうか
これはbatch_normをモデルの層に追加していないものでの学習結果だが、追加したものは収束がのんびりで、かなりのエポック数を回せばいい感じの形状が得られそうだと試して思った。

当たり前だがハイパーパラメータやユニットの初期値の設定がかなり大事何だろうか
GANのより良い学習方法については論文があるらしいので読んで改善したい

地味に損失の定義式で関数名と引数名が長すぎて途中で定義式をぶった切る形にしないといけなかったのがムズムズした

追記

世の中には Google Colaboratory という便利なものがあるそうでGPUを使って学習できるように改造した。
チェックポイントも作るようにした賢い

ソースはここ

10エポックほど回してみてCPUでの学習とどれくらい変わるのか計測して見た
f:id:Owatank:20180421170818p:plain

まあ・・・こんなもんすよ・・・