2017-12-19

線形代数のまとめ　その１(線形空間、基底とか)

線形代数

プログラミングのための線形代数という本で線形代数の復習をしている。4章あたりまで読んだので振り返りとしてメモを残すことにする。

よく変数で配列だったりタプルだったりを使うことがある。これは複数の数値や文字列の集まりを一つのものとして見る。物理や線形代数だったりの勉強をしているとそれらはベクトルと呼ばれてる。
f:id:Owatank:20171219101249p:plain
こんなやつ。大学だと矢印じゃなくて太字で書くものしか見ない...

ベクトルでは同じ次元(上で言うとnの値)のもの同士なら足し算(引き算)と定数倍ができる。
例えばこんなベクトルがあるとして
3人の現在の身長 = (1.5m,1.8m,1.7m)
3人の2年前の身長 = (1.4m,1.6m,1.5m)

3人の2年前から伸びた分の身長を求めたいとする。これは現在の身長から2年前の身長を引いて残ったものが伸びた分になるから

3人の2年前から伸びた分の身長 = 3人の現在の身長 - 3人の2年前の身長
= (1.5m - 1.4m , 1.8m - 1.6m , 1.7m - 1.5m)
= (0.1m , 0.2m ,0.2m)

3人の2年前から伸びた分の身長= (0.1m , 0.2m ,0.2m)となる。

定数倍は
3人の現在の身長を3倍したもの = 3*(3人の現在の身長)と表せることができて

3人の現在の身長を3倍したもの = 3*(3人の現在の身長)
= 3*(1.5m,1.8m,1.7m)
= (3*1.5m,3*1.8m,3*1.7m)
= (4.5m,5.4m,5.1m)

ベクトルを構成している各要素を c倍すればいい

掛け算や割り算もできそうじゃんって思うけど、できない
3人の現在の身長(cm表記) = (150cm,180cm,170cm) 3人の2年前の身長(cm表記) = (140cm,160cm,150cm) 先ほどのベクトルをcm表記で表したものを用意する。

この2つから3人の2年前から伸びた分の身長(cm表記)と3人の現在の身長を3倍したもの(cm表記)を求めると

3人の2年前から伸びた分の身長(cm表記) = 3人の現在の身長(cm表記) - 3人の2年前の身長(cm表記)
= (150m - 140cm , 180cm - 160cm , 170m - 150cm)
= (10cm , 20cm , 20cm)

3人の現在の身長を3倍したもの(cm表記) = 3*(3人の現在の身長(cm表記))
= 3*(150cm,180cm,170cm)
= (3*150cm,3*180cm,3*170cm)
= (450cm,540cm,510cm)

表記は違うけど、求めたいものの意味合い(数値)は同じ

(3人の現在の身長)x(3人の2年前の身長)と(3人の現在の身長(cm表記))x(3人の2年前の身長(cm表記))は同じになるか考える

(3人の現在の身長)x(3人の2年前の身長)
=(1.5*1.4, 1.8*1.6, 1.7*1.5)
=(2.1m, 2.88m, 2.55m)

(3人の現在の身長(cm表記))x(3人の2年前の身長(cm表記))
=(150*140, 180*160, 170*150)
=(21000, 28800, 25500)  //m表記に直すと
=(21m, 28.8m, 25.5m)

足し算や定数倍は同じものだったのに掛け算は全く別物になってしまった。
こんな風に掛け算と割り算はcmをmに直すといった座標系と呼ばれるものを変更するとxy = zがx'y' ≠ z'という感じになってしまうからできない。というよりは成立するかわからないからできない。

元に戻って「足し算(引き算)」と「定数倍」が定義された世界のことを線形空間またはベクトル空間と呼ぶ。
ベクトルというのは以下のように矢印のようなもので表すことができる。(x軸とy軸で構成する2次元空間とする)
f:id:Owatank:20171219105321p:plain
これは $\vec{v}$ という場所にはx座標に3歩進んで、y座標に2歩進むことで到着できる を表す

ちょっと待ってほしい。この方眼紙のような目盛りって誰が用意したのだ

もしこの目盛りがなくなったとして、こんな状況を考える
f:id:Owatank:20171219112038p:plain 誰かに $\vec{v}$ の地点までお使いして欲しいとき、行き方はどうやって教えればいいだろう
目盛りがないと3コマ目のようにどの方向にどんな歩幅で3歩、2歩進めばいいか悩んでしまう。

目盛りがないなら、自分で作ればいいじゃん！ということで基準(目盛り)となるベクトル ${ \displaystyle \vec{e_1},...,\vec{e_n} }$ を定める。

基準を決めてしまえば、それを使って $\vec{v}$ への行き先を「 $\vec{e_i}$ の方向に3歩、 $\vec{e_j}$ の方向に2歩進む」と伝えることができる。

f:id:Owatank:20171219113911p:plain

ベクトルは足し算、定数倍できることはわかったから $\vec{v} = 3\vec{e_i} + 2\vec{e_j}$ と書ける。
つまり $\vec{v}$ は $\vec{e_i}$ と $\vec{e_j}$ という基準の組み合わせで表現できるということ。

「基準となる1組のベクトル」を基底、「各基準で何歩進むか」を座標と呼ぶ。
上の例だと「基底 $(\vec{e_i},\vec{e_j})$ に関して、ベクトル $\vec{v}$ の座標は $\vec{v}=(3,2)^{T}$ 」
ここでは基底は $(\vec{e_i},\vec{e_j})$ の組であり、各要素 $\vec{e_i}$ 、 $\vec{e_j}$ のことを基底ベクトルという。

基底という目盛りを自分で作れることがわかったけど、基底 $\vec{e_1},...,\vec{e_n}$ を作るにも条件がある。

(今考えている線形空間内の)どのベクトル $\vec{v}$ でも $\vec{v} = x_1 \vec{e_1} + ... + x_n \vec{e_n}$ という形で表せること(x1,...,xnは任意の数)
その表し方は一通りであること

一つ目は特定のベクトルだけ表せる基底なんて基底と言えない。二つ目は表し方が一通りでないと、異なる座標 $\boldsymbol{x}=(x1,...,xn)^{T}$ と $\boldsymbol{y}=(y1,...,yn)^{T}$ が与えられたときそれが違うもの同士か同じものが2通りの書き方をされているか困ってしまうことがあるから

2次元空間において以下のようなものが基底として取れる
f:id:Owatank:20171219121200p:plain
2本の基底ベクトルが「独立した方向」を向いていること
この独立という単語がいまいち難しいかもしれないけど、後々大事になってくる

以下のようなものは基底として取れない悪い例
f:id:Owatank:20171219121642p:plain

左は1本の基底ベクトルでは無理ということ
2次元空間なのに1本の基底ベクトルでは(x軸、y軸としたら)片方の軸しか表すことが出来ないから。これは基底の条件である
どのベクトル $\vec{v}$ でも $\vec{v} = x_1 \vec{e_1} + ... + x_n \vec{e_n}$ という形で表せることという条件を破ってしまう
真ん中は2次元空間において3本(以上)の基底ベクトルは余分ということ
$\vec{e_k}$ という基底ベクトルは $\vec{e_i}$ は $\vec{e_j}$ で表すことができるから必要ない。(基底の組として要素にする必要がない)
右は2本の基底ベクトルが同じ方向ではダメということ
$\vec{e_i}$ を c倍すれば $\vec{e_j}$ になるから $\vec{e_j}$ は余分
結局1本の基底ベクトルだけということになる。これは基底の条件の一つ目を破ってしまうのでダメ

数学的な表現では

$u_1 \vec{e_1} + ... + u_n \vec{e_n} = \vec{0}$ 　ならば　 $u_1 = ... = u_n = 0$

与えられたベクトル $\vec{e_1},...,\vec{e_n}$ に対して、任意の数 $u_1 , ... , u_n$ を用意してできるベクトル
$u_1 \vec{e_1} + ... + u_n \vec{e_n}$ を $\vec{e_1},...,\vec{e_n}$ の線型結合をよぶ
複数のベクトルを n倍だったり m倍して足したり引いたりしたものをその複数のベクトルの線型結合というんだな

これらの条件から基底は「 $\vec{e_1},...,\vec{e_n}$ の線型結合で任意のベクトル $\vec{v}$ が表現できて、その表し方が一通り(唯一)であるとき、 $(\vec{e_1},...,\vec{e_n})$ を基底と呼ぶ」

おまけで次元数は基底ベクトルの本数から定義されるので
次元　＝　基底ベクトルの本数　＝　座標の成分数 と定義される。

長くなったのでここまで

2017-12-12

チコノフ(Tikhonov)正則化について

お久しぶりです。

最近プログラミングのための線形代数という本で線形代数のやり直しをしている。基底のイメージが掴みやすくて読んでいて楽しい

第二章の最後あたりにチコノフ正則化というものについて書いてあったので試してみることにした
コードはいつも通りここ(リンクを修正)

github.com

線形代数をやったことある人は以下の数式をよく見かけるはず
f:id:Owatank:20171212154859p:plain
(y,xはベクトル、Aは行列)

何をしているかというと(m,n)行列Aでn次元のベクトルxをm次元のベクトルyへと写像している
写像という言葉がイメージを掴みにくいけれど、m=3,n=2(m>n) に設定するとして

2次元空間で表されるベクトルxという平面を3次元空間に移す(写像する)とき、その空間でベクトルxはどのように表現されるかということ、であってるはず

f:id:Owatank:20171212160305p:plain

図で表すとこうなる。y=Axから元の2次元平面にある点xは写像した結果3次元空間ではyというベクトルで表される。図から写像した赤い平面以外の場所にある点(zとする)へと移れるxは存在しないことがわかる。こういう場合は単射というそうだ。

もちろん逆の場合m=2,n=3(m<n)も考えられる。3次元ベクトルで表されるxが2次元空間へ写像したときどう表現されるかということ。3次元情報を2次元情報で表すのは無理があるのでいくつか情報は削られてしまう。マリオがペーパーマリオになってしまう感じだ。

なので写像するときにはn次元からn次元への写像が基本的に嬉しい。n次元ベクトルxを回転したり引き延ばしたりする写像Aで写した時のn次元ベクトルyとか考えやすい。

n次元からn次元への写像において y = Ax とすると、yからxに戻すときは逆行列 inv_A を用いれば元に戻れる。 f:id:Owatank:20171212161825p:plain

このことから写像する行列Aには逆行列が存在しないといけないこともわかる。(行列Aは正則行列でなくてはならないということ)
逆行列が存在しないということはn次元空間を作るためのn本の基底が存在しない(n-1本だったりとか)ということで上の3次元情報を2次元情報で表現するといった状況になっていることになる。

世の中はひねくれているので正則行列ではあるけどほぼ逆行列に近い行列Aというのも存在する。
立方体をほぼ平面にするくらいぺちゃんこにしてしまう行列Aとかそんな感じ。このとき逆行列は元の立方体に戻す行列だからぺちゃんこな立方体を物凄く拡大して戻す逆行列 inv_A となる。

ここで元の立方体にノイズ(立方体の箱に黒い点のような落書きをしておくイメージ)を乗せて上のようなほぼ逆行列に近い行列Aでぺちゃんこにして、 inv_A で元に戻した時、ノイズも物凄く拡大されてしまう(黒い点のような落書きがかなり引き伸ばされたりしているイメージ)問題が発生すると本に書いてあった。

試してみることに
元の画像は以下のカニさん f:id:Owatank:20171212162928p:plain

画像を多少ぼかす行列Aを用意する
f:id:Owatank:20171212163027p:plain
単位行列の対角成分周りをぼやぼやした感じ(0.13とか0.6とか値を小さく)調整した。

y = Ax としたときのyの結果はこうなった
f:id:Owatank:20171212163245p:plain

全体的に暗くなった感じもあるけどちょっとぼやけてるのがわかる。
このyにノイズを乗せる(y+noise)
f:id:Owatank:20171212163402p:plain

Aの逆行列をかけて元に戻す( x = inv_A(y+noise) )

f:id:Owatank:20171212163815p:plain

かなりザリザリした結果になった。ノイズが引き伸ばされたのはわかる。
ちなみに逆行列自体はこんな感じだった
f:id:Owatank:20171212163911p:plain
なんかロマンチックだ

このノイズが引き伸ばされるのをなんとかしようというのがチコノフ正則化で、ざっくりいうと Ax と y+noise の距離(|| Ax - y ||)とか正則項を適用したりして、いい感じになるxを決めるぽかった。数式で表すとこうなる
f:id:Owatank:20171212165419p:plain

右辺のyを除いた行列の結果は以下のようになった(α=0.03)
f:id:Owatank:20171212165921p:plain
逆行列 inv_A を表したものを太くした感じに見える

これをノイズありのyにかけるとこうなる
f:id:Owatank:20171212170052p:plain

ちょっとノイズが減ったのがわかる。でも完璧にとはいかなかった。αを0.5とかに変えたりすると元の画像xではなくどちらかというとぼかし行列を加えたyに近くなった。
この原因はなんだろう。逆問題あたりをもっと調べるとわかってくるのだろうか。

2017-11-21

Dropoutのハイパーパラメータの決定について

機械学習

ここ1ヶ月ほど、会社のアルバイトで6クラスの画像分類モデルをTensorflowを使って作ることを任された
色々詰まった、考えさせられたことがあったのでメモ

画像分類だったらCNNで、ネットワークはVGG16だったりAlexNetで作りましたべろ〜んwって感じでいいと思うが、そのモデルをProtocolBufferファイルにしてラズパイなどに乗せて動かすということなのでネットワークの層が深すぎるとProtocolBufferファイルが400~700MBになって重すぎて敵わん...となってしまうので6層ほどで適当に作ることにした

f:id:Owatank:20171121151707p:plain

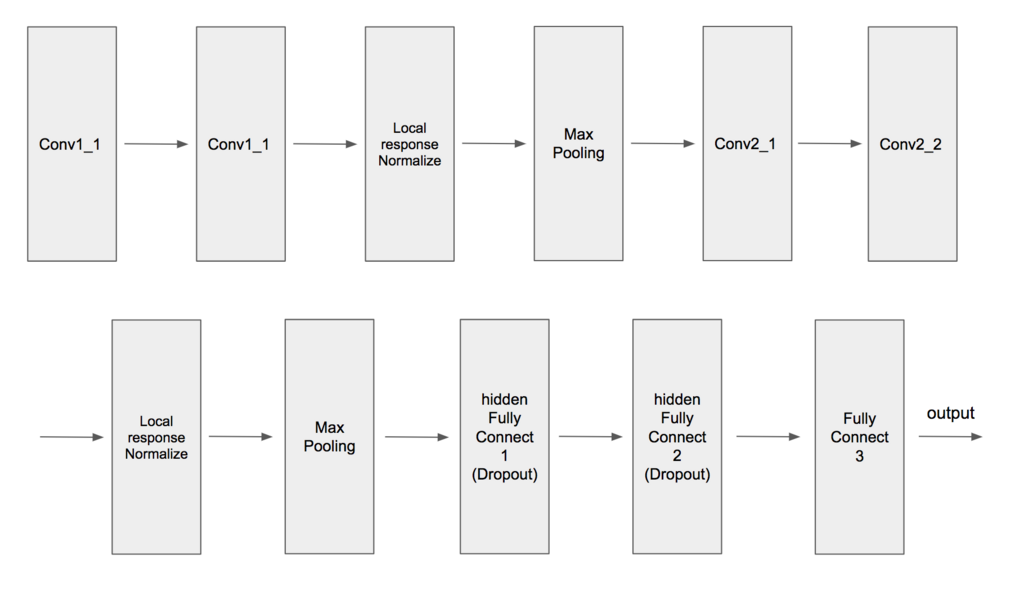
~~全然6層じゃなかった~~
畳み込みのkernel_sizeは3~5で、Dropoutは0.5で調整した

いざ学習させたらなぜか学習が進まなかった。損失は減っているが精度が0.23~0.25間で向上しなかった。
別の2層の畳み込み層と2層の全結合層のモデルは学習が進んでいたことから、自分のモデルのパラメータの設定がおかしいのだろうかと悩んだ
畳み込み層、学習係数のハイパーパラメータは同じだったので、全結合層のパラメータやLocal response Normalization層が原因なのかと考えたりした

試行錯誤した結果、上記のせいで学習が滞っていたのではなく、Dropoutのパラメータが原因だったということがわかった
上のネットワーク図からわかるように2つの隠れ層である全結合層にはDropoutを適用している。どちらもkeep_probは0.5に設定した
このkeep_probをどちらも0.8に変更した結果、学習が進んだ

Dropoutについては青いイルカさんの本とかでは仕組みや嬉しいことの説明はあったが最適なパラメータの設定値の説明はなかった。なのでいつも0.5で設定していた
調べたところ最初に来る全結合層に対してDropoutを適用するとき、そのパラメータを0.5にするのはあまり良くないそうだ

sonickun.hatenablog.com

というわけで学習が進まない問題は回避できてなんとかなった

その後、全結合層のノード数とDropoutのkeep_probパラメータの間に何か関係があるのか気になったので調べることにした
使うデータはTensorflowのチュートリアルで有名なMNISTで全結合層のみのネットワークを構築した

mport tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

t = tf.placeholder(tf.float32, shape=(None,10))
X = tf.placeholder(tf.float32, shape=(None,28*28),name="input")
keep_prob_1 = tf.placeholder(tf.float32) # ドロップアウトする割合
keep_prob_2 = tf.placeholder(tf.float32) # ドロップアウトする割合

stddev = np.sqrt(2.0 / 28*28)
h_W1 = tf.Variable(tf.truncated_normal([28*28,256], stddev=stddev))
h_b1 = tf.Variable(tf.constant(0.1, shape=[256]))
h_fc1 = tf.nn.relu(tf.matmul(X,h_W1) + h_b1)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob_1)

stddev = np.sqrt(2.0 / 256)
h_W_fc2 = tf.Variable(tf.truncated_normal([256,512], stddev=stddev))
h_b_fc2 = tf.Variable(tf.constant(0.1, shape=[512]))
h_fc2 = tf.nn.relu(tf.matmul(h_fc1_drop, h_W_fc2) + h_b_fc2)
h_fc2_drop = tf.nn.dropout(h_fc2, keep_prob_2)

stddev = np.sqrt(2.0 / 512)
W_fc3 = tf.Variable(tf.truncated_normal([512,10], stddev=stddev))
b_fc3 = tf.Variable(tf.constant(0.1, shape=[10]))
fc3 = tf.matmul(h_fc2_drop, W_fc3) + b_fc3
p = tf.nn.softmax(fc3,name="output")

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=fc3, labels=t))

optimizer = tf.train.AdamOptimizer(1e-4)
train_step = optimizer.minimize(loss)

correct_prediction = tf.equal(tf.argmax(fc3,1), tf.argmax(t,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

saver = tf.train.Saver()

### 学習の実行
sess = tf.Session()
sess.run(tf.global_variables_initializer())
i = 0
for i in range(0,10000):
    batch = mnist.train.next_batch(30)
    sess.run(train_step, feed_dict={X:batch[0],t:batch[1],keep_prob_1:0.5,keep_prob_2:0.5})
    if i % 1000 == 0:
        train_acc, train_loss = sess.run([accuracy,loss], feed_dict={X:batch[0],t:batch[1],keep_prob_1:1.0,keep_prob_2:1.0})
        print("[Train] step: %d, loss: %f, acc: %f" % (i, train_loss, train_acc))
        # テストデータによるモデルの評価
        test_acc, test_loss = sess.run([accuracy,loss], feed_dict={X:mnist.test.images,t:mnist.test.labels,keep_prob_1:1.0,keep_prob_2:1.0})
        print("[Test] loss: %f, acc: %f" % (test_loss, test_acc))

        saver.save(sess, "./ckpt/mnist")
sess.close()

h_fc1とh_fc2にdropoutを適用したりしなかったり、keep_prob_1とkeep_prob_2の値を変えて訓練結果を確認した
まずh_fc1とh_fc2のノード数が、48,96でdropoutを適用しなかった時の結果(多いので2000step毎だけ)

[Train] step: 0, loss: 15.007373, acc: 0.066667
[Test] loss: 12.547914, acc: 0.097100
[Train] step: 2000, loss: 0.960308, acc: 0.666667
[Test] loss: 0.894258, acc: 0.735600
[Train] step: 4000, loss: 0.381689, acc: 0.800000
[Test] loss: 0.603150, acc: 0.818700
[Train] step: 6000, loss: 0.460051, acc: 0.866667
[Test] loss: 0.484288, acc: 0.855700
[Train] step: 8000, loss: 0.595815, acc: 0.866667
[Test] loss: 0.419885, acc: 0.873900

精度はいまいち...次にノード数はそのままでdropoutを適用し、keep_prob_1、keep_prob_2が共に0.5に設定したとき

[Train] step: 0, loss: 18.346718, acc: 0.033333
[Test] loss: 12.756997, acc: 0.122000
[Train] step: 2000, loss: 1.504397, acc: 0.500000
[Test] loss: 1.692765, acc: 0.451800
[Train] step: 4000, loss: 1.380499, acc: 0.566667
[Test] loss: 1.422444, acc: 0.552400
[Train] step: 6000, loss: 1.460326, acc: 0.600000
[Test] loss: 1.400168, acc: 0.609900
[Train] step: 8000, loss: 1.548799, acc: 0.533333
[Test] loss: 1.289341, acc: 0.667200

適用なしの時より悪化しているのがわかる

色々試した結果、keep_prob_1は1.0(dropoutを適用しない)keep_prob_2を0.8に設定した結果がdropout適用しないときより良かった

mnist-dropout-48-96-10-08-ckpt

[Train] step: 0, loss: 17.872959, acc: 0.066667
[Test] loss: 16.914766, acc: 0.103000
[Train] step: 2000, loss: 1.499189, acc: 0.666667
[Test] loss: 1.236634, acc: 0.663800
[Train] step: 4000, loss: 0.986408, acc: 0.666667
[Test] loss: 0.778916, acc: 0.762500
[Train] step: 6000, loss: 0.436568, acc: 0.866667
[Test] loss: 0.605089, acc: 0.813300
[Train] step: 8000, loss: 0.290827, acc: 0.933333
[Test] loss: 0.504056, acc: 0.846000

次に上記の結果はノード数が少なすぎるからkeep_prob_1、keep_prob_2が共に0.5の結果は悪かったのでは？と疑問に思い、各ノード数を256,512にした時でも同様に結果を観察することにした
まずはdropout適用しないときの結果

[Train] step: 0, loss: 9.332975, acc: 0.166667
[Test] loss: 10.855021, acc: 0.127700
[Train] step: 2000, loss: 0.380751, acc: 0.966667
[Test] loss: 0.349467, acc: 0.905500
[Train] step: 4000, loss: 0.222563, acc: 0.966667
[Test] loss: 0.241931, acc: 0.931800
[Train] step: 6000, loss: 0.108663, acc: 0.966667
[Test] loss: 0.199128, acc: 0.943000
[Train] step: 8000, loss: 0.077383, acc: 0.966667
[Test] loss: 0.172284, acc: 0.948200

元々の表現力が上がったせいか48,96のときより精度が良くなっている
次にkeep_prob_1、keep_prob_2が共に0.5のときの結果

[Train] step: 0, loss: 7.612897, acc: 0.200000
[Test] loss: 9.190090, acc: 0.129300
[Train] step: 2000, loss: 0.934076, acc: 0.733333
[Test] loss: 0.541602, acc: 0.850500
[Train] step: 4000, loss: 0.303545, acc: 0.966667
[Test] loss: 0.453306, acc: 0.869100
[Train] step: 6000, loss: 0.434249, acc: 0.900000
[Test] loss: 0.529966, acc: 0.884700
[Train] step: 8000, loss: 0.707538, acc: 0.866667
[Test] loss: 0.521837, acc: 0.899100

精度自体はdropoutなしの方より悪い気するけど48,96でkeep_prob_1、keep_prob_2が共に0.5のときの結果と比べて、学習が停滞しているようには感じない
やはりノード数が多いからだろうか？

最後にkeep_prob_1は1.0(dropoutを適用しない)keep_prob_2を0.8に設定した結果

[Train] step: 0, loss: 15.822262, acc: 0.000000
[Test] loss: 15.912350, acc: 0.069200
[Train] step: 2000, loss: 0.096453, acc: 0.966667
[Test] loss: 0.338137, acc: 0.914300
[Train] step: 4000, loss: 0.138627, acc: 0.966667
[Test] loss: 0.221914, acc: 0.936700
[Train] step: 6000, loss: 0.005314, acc: 1.000000
[Test] loss: 0.170819, acc: 0.948000
[Train] step: 8000, loss: 0.288768, acc: 0.866667
[Test] loss: 0.142067, acc: 0.958000

dropoutなしよりとても良くなった

Dropoutのパラメータの設定でここまで結果が変わるとは思っていなかったので調べてて面白かった

2017-11-03

ベイズの定理とソフトマックス関数について

機械学習

授業が始まって中々勉強に時間が取れないがちょっとだけPRML上巻を読んだ。
ベイズの定理について自分なりの解釈としてのメモをかくことに

中学で確率における同時確率(または結合確率)というのを習った。これは事象XとYがあるとして、XとYが同時に起こる確率を示したもの。数式で表すとこうなる
f:id:Owatank:20171103114224p:plain

重要なのはこの等式は事象XとYが独立のとき成立するということ。
XとYが独立であるとは、片方の事象が起こる可能性がわかっていても、もう片方の可能性に何も影響しないということを意味している。

独立の場合は上の等式のようにそれぞれの事象の確率の積で同時確率を計算できる。
中学の問題で言えば裏表のコインやサイコロを振るとかがあった。

実際の状況、問題においては独立でない場合の事象を考えることが多いからこの等式では同時確率を求めるのは難しい。困った。

そこで、事象の依存性を考慮した同時確率を考える。これは以下のようになる。
f:id:Owatank:20171103115117p:plain

確率の乗法定理と呼ばれる。この式が意味することは「事象XとYが同時に起こる確率」は「Xが起こる確率」と「Xが起きた時にYが起こる確率」の積で求められるということ。

右辺にあるP(Y|X)は「Xが起きた時にYが起こる確率」からYの事前確率だったりYの条件付き確率だったり呼ばれる。らしい。。

またこの乗法定理において事象XとYが独立とわかっているなら、P(Y|X)はP(Y)と書き換えることができる。

最初この乗法定理を見た時、Yの事前確率にP(X)というXが起こる確率で重み付けしたものが、同時確率P(X,Y)になると考えてしまった。
機械学習の勉強をしているとどっかしらの項を重みと見てしまう悪い発作だ。。。

同時確率P(X,Y)はP(Y,X)と書き換えることもできる。そしてこんな感じになる。
f:id:Owatank:20171103120721p:plain

つまり以下の関係が得られる。
f:id:Owatank:20171103120827p:plain f:id:Owatank:20171103120908p:plain

2枚目の方は有名なベイズの定理。何度も見て何度も忘れた。

式だけを見れば、「Yの事後確率」は「Yの起こる確率」と「Xの事後確率」を掛け合わせたものを「Xの起こる確率」で割ったもので求めることができる、という意味になる。
f:id:Owatank:20171103121624g:plain
正直こんな感じだ。でも嬉しいことはおそらくP(Y|X)を求めるには他の3つの確率を調べれば良いということなんだろう。

こういう時は例で考える。事象Xを年間の行事と考える。ハロウィンだったりプレミアムフライデーだったり色々だ。そして事象Yを美味しい料理と考える。これもケーキだったり厚焼き玉子だったり寿司だったり色々ある。

ある人がクリスマスでうきうきしていて、ケンタッキーのフライドチキンを食べたいとする。その人は「そもそもクリスマスのとき、ケンタッキーのフライドチキンがでる確率っていくらぐらいなんだ・・・？」と疑問に思ったので調べたいとする。

f:id:Owatank:20171103151948p:plain

つまりP(Y=ケンタッキー|X=クリスマス)を求めたい。
求めるにはクリスマスに出てくる全ての料理を挙げて、そのうちケンタッキーがどれくらいの割合を占めるかを考えないと求めることはできない。

ベイズの定理から、他の3つの確率で求めてみる。

P(Y)はケンタッキーが出てくる確率。年間の売り上げ数から求められるはず。
P(X|Y)はケンタッキーが出てきたとき、その日の行事がクリスマスである確率となる。これもケンタッキーの年間売り上げからクリスマスの日がどれだけの割合を占めているかで求められそうだ。
P(X)はクリスマスが起こる確率。クリスマスは年に一度のため悩む必要はない。

P(Y=ケンタッキー|X=クリスマス)で求めるか、他の3つの確率で求めるか、どちらのが簡単だろうか。
前者はクリスマスに出てくる全ての料理を挙げ切るのはとても厳しい気がする。後者も大変かもしれないがケンタッキーの年間売り上げあたりを調べればいいだけだ。

P(Y|X)の測定が難しいなら、他の容易な3つの確率から求めることができる。すごいぞベイズの定理。

もう一つ疑問に思ったことがある。ベイズの定理の右辺にある分母のP(X)は何をしているのだろうか。
純粋に式だけを見ればP(Y)P(X|Y)を割っているだけだが、なぜ割ればP(Y|X)が求まるのだろう。。そういう定理だからで片付くが今いちしっくりこない。

右辺の分母について考える。P(X)は「Xが起こる確率」だが「事象Yの値に関係なく事象Xが起こる確率」とも言える。これは式で表すと

f:id:Owatank:20171103142901p:plain

Nが表すのは上の例(事象Yを美味しい料理)で言うならば y1 = ケーキ、 y2 = 玉子焼き、... といった事象Yが取りうる数。
P(X=クリスマス,Y=ケーキ) + P(X=クリスマス,Y=卵焼き) + ... P(X=クリスマス,Y=yj)まで事象Xがクリスマスの時に起こりうる同時確率の総和がP(X)だ。

P(X)をこの数列で表した時のベイズの定理はこうなる
f:id:Owatank:20171103143509p:plain

分子は事象X=クリスマス、事象Y=ケンタッキーの同時確率なのでこう書き換えられる
f:id:Owatank:20171103143552p:plain

こうみるとどうだろう。分子は分母の数列の中にある一部の同時確率である。
これは(全体の一部、あるいは比べる量) ÷ (元、全体の量)といった割合として見ることができるじゃないか。
百分率ではないので右辺の値は必ず [0,1] 範囲に収まる。確率としての値が出てくる。

分母のP(X)は右辺が [0,1] 範囲に収まるようにある意味での正規化としての役割を担ってくれていたのだ・・・

そしてこの時何かに似ていると気づいた。ニューラルネットワークの活性化関数の一つであるソフトマックス関数のことである。
分類問題における出力が [o1,o2,...,on]となっているとき、ソフトマックス関数を適用すると各出力の総和が 1 になるように o1,o2,..,onを変換してくれる。
ベイズの定理にある分母のP(X)と同じように正規化をしてくれる。

青いイルカの深層学習本ではベイズの定理の説明がなかったので~~自分がベイズの定理についてあやふやだった~~ソフトマックス関数のとこは「ほーん」って感じに読んでいたがベイズの定理がベースになってるじゃーんと今さらだが興奮した。

2017-10-23

KaggleのTitanicで上位10%に入った手法のまとめ

機械学習

初心者向けですが深層学習の講師を最近やりました。
講義の中で実際にKaggleのコンペで腕試しをするということをしたかったので講義をやる前にチャレンジした。

今回腕試しをするコンペはkaggleのチュートリアルで有名なtitanicを選んだ。

Titanic: Machine Learning from Disaster | Kaggle

どういった内容かというと、タイタニック号の乗客のデータからある乗客は生存したか否かを判定し、その正解率を競う感じ。
試行錯誤して自分の最高スコアは 0.81339 になった。上位10%だしそこそこ頑張れたはず。
f:id:Owatank:20171023141813p:plain

もう少し上を目指したいとこだが授業も始まったので一旦打ち切り
コードはここ

github.com

データ分析にはpandasを用いた。最初はdescribe()やdf.isnull().sum()とかで統計や欠損値の確認をする。
f:id:Owatank:20171023142710p:plain
訓練データのAge、Cabinなどに欠損値があるのがわかる。

次に仮説をいくつか立ててその条件でデータを操作し、その時の生存者の割合を確認していった。仮説は主に

子供や赤ん坊など年齢が若い人の方が優先して救助されるのではないか
女性のが優先して救助されるのではないか
Pclass1(だいたいお金持ちの乗客)の人たちは優先して救助されるのではないか

などなど

年齢はやっぱりというか子供のが生存率が高いのは確認できた
f:id:Owatank:20171023144512p:plain

生存率に関しては性別の違いが一番別れていた。
f:id:Owatank:20171023144812p:plain

後は名前の属性を何かしら使いたい(文字列の操作を練習したかった)ので名前からMrやMissなどを抽出してそれらの生存率を確認したりした。

f:id:Owatank:20171023143804p:plain

生存の判別モデル構築の問題として年齢を特徴として扱いたいけど欠損している乗客がいる。
この問題に対して訓練データの年齢における欠損値を除いた年齢の中央値で穴埋めか年齢自体を予測するモデルを作り、そのモデルの予測結果で穴埋めするといった2つの手法をとった。

良い精度が出たのは後者の方だった。年齢予測モデルはXGBoostで構築した。

最終的に使う特徴はこれらに絞った
f:id:Owatank:20171023150053p:plain

one_hot系は文字列カテゴリを数値に変換したもの
SibParchはSibSpとParchを合わせたもの
Fare_rounddown_splitはFareの小数点を打ち切り、10ドルごとにカテゴリ分けしたもの
By_Age_classはAgeを10歳ごとにカテゴリ分けしたもの

生存者の判別モデルとしてTensorflowでロジスティック回帰モデルとXGBoostモデルの2つを構築し、比較した。

Tensorflowのロジスティック回帰モデルは以下のように構築した

# 入力層
X = tf.placeholder(tf.float32, shape=[None, 7], name="input")
t = tf.placeholder(tf.float32, shape=[None, 1])
# パラメータ1
stddev = np.sqrt(2.0 / 7)
W1 = tf.Variable(tf.truncated_normal([7,24], stddev=stddev))
b1 = tf.Variable(tf.constant(0.1, shape=[24]))

# パラメータ2
stddev = np.sqrt(2.0 / 24)
W2 = tf.Variable(tf.truncated_normal([24,48], stddev=stddev))
b2 = tf.Variable(tf.constant(0.1, shape=[48]))
keep_prob = tf.placeholder(tf.float32) # ドロップアウトする割合

# パラメータ3
stddev = np.sqrt(2.0 / 48)
W3 = tf.Variable(tf.truncated_normal([48,1], stddev=stddev))
b3 = tf.Variable(tf.constant(0.1, shape=[1]))

layer1 = tf.nn.relu(tf.matmul(X,W1) + b1)

layer2 = tf.nn.relu(tf.matmul(layer1,W2) + b2)
layer2_drop = tf.nn.dropout(layer2, keep_prob)

layer3 = tf.matmul(layer2_drop,W3)+b3

p = tf.nn.sigmoid(layer3,name="output")
# 荷重減衰
norm_term = tf.nn.l2_loss(layer1) + tf.nn.l2_loss(layer2_drop)
# 正則項
lambda_ = 0.001
# 損失関数
loss = tf.reduce_mean(tf.square(p - t))+ lambda_*norm_term
# 学習アルゴリズム
optimizer = tf.train.AdamOptimizer()
train_step = optimizer.minimize(loss)
# 精度
correct_prediction = tf.equal(tf.sign(p-0.5), tf.sign(t-0.5))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

XGboostとlog_lossで誤差の値を比べたがXGboostの勝利だった
NNと決定木における表現力の問題だろうか・・・

ハイパーパラメータをいじって提出していたら 0.81339 という結果が出た。

終わった後に他の人と話してタイタニックは実際にあった話、つまり背景があるから背景から得られる情報を使えばよかったとか元のタイタニック号の船構造を見つけて救命艇がどこにあるかや部屋番号の割り当て(Cabin)を確認するのもアリだったよねーとか灯台下暗しって感じに知見を得た。

他にもstackingや交差検証など学習方法の見直しも大事

2017-10-13

物体検出の実装を目指す-Fast R-CNNについて

機械学習

結構間が空いたが、Fast R-CNNの論文を読んだ。適度にメモする。

SPPnetではSelectiveSearchから得た候補領域一つ一つをCNNにかけるというのを無くし、対象とする画像データ一枚からCNN(畳み込みの処理のみ)にかけて得た特徴マップから物体検出を行う手法をとることで、大幅な時間短縮に成功した。大体RCNNから24~102倍(テスト時)速くなった。

Fast-RCNNはSPPnetより10倍(テスト時)速くなっている。まだ速くなるのか。

物体検出は画像分類と比べて複雑な2つの主要な課題がある。(というよりは発生する)

SelectiveSearchなどで候補領域を処理しなければいけないこと
これらの候補領域は正確な位置特定を達成するための大まかな位置情報しか提供しないこと。つまり洗練しなければいけない。

Fast-RCNNではこの2つの問題を考慮し、物体の候補領域から分類を行うこと、空間的位置を改善することを共同で学習する単一段階のアルゴリズムが導入されている。
やっと分類と位置特定の2つが一度に学習できる段階に来た。これは胸が熱い。。。

SPPnetも十分すごいが、かなり大きい欠点がある。それはSPP層つまり空間ピラミッドプーリング処理より前の畳み込み層を更新することができないということ。この欠点によってディープネットワークの精度に限界が発生してしまう。

Fast-RCNNではこの問題も解決しており、全てのネットワークの層を更新できる。

学習の手順としては以下のようになる。

f:id:Owatank:20171013125712p:plain

SPPnetと同様に画像全体と物体の候補位置を受け取り、画像全体から畳み込み層と、Maxプーリング層にて一枚のConv特徴マップを生成する。

次に、その特徴マップから受け取った各候補位置に対応する領域を抜き出し(RoI Projectionのあたり)、RoI(region of interest)プーリングと呼ばれる処理を行い固定長の特徴ベクトルを出力する。
出力した固定長の特徴ベクトルは2つのfc層に分岐する。

一つ目はクラス分類を行う出力のsoftmaxに
二つ目はより洗練されたbounding-boxの位置を符号化するbbox-regressorへ

Fast-RCNNにて新たにRoIプーリングが出てきた。これは簡単にいうとSPP層におけるピラミッドレベルが一つしかないプーリング処理。どっちも任意の領域内で決まった長さの特徴ベクトルを出力することに変わりはない。

f:id:Owatank:20171013133646p:plain

そして分類とbounding-box回帰の訓練において2つを合わせたマルチタスクの損失関数を定義することでこの2つを共同に訓練することができる。
またこのマルチタスクの損失関数の定義によって全てのネットワークの層を更新することが可能となった。すごいぞお

次はいよいよFaster-RCNN

参考文献及び画像(Fast-RCNNの論文先)

2017-10-09

SECCON Beginners2017 東京に行ってきた感想

CTF

f:id:Owatank:20171009134445p:plain

滅多に人が来ないこのブログのアクセス数が1000超えてた。あったけえ・・・
ベリベリサンクスヾ(≧∀≦)ﾉ

タイトル通りctf4bの東京会場行ってきた。去年の2月くらいにCicada3301という話をネットで読んですごいワクワクして謎解きみたいで面白そうと思い、その後で似たような感じのCTFというものを知った。

機械学習の方の勉強を優先していたのでCTFの勉強に時間は取れてなくて初心者向けの講義受けて見たいと申し込みしたら当選してびびった。

内容としては最初にセキュリティに関しての倫理の話から始まってWeb、フォレンジック、リバースエンジニアリングの講義があった。

Web

検証ツールを使ったソースコードから手掛かりを探す方法や脆弱性の種類についての説明があった。
Request/Response Headerにも手掛かりがあるとは知らなかった。
あとはSQLインジェクションだったり、Directory Traversal、Local File Inclusionなどについても説明があった。
Djangoのデバッグモードからソースコードを入手してflagを取得する解法もあったりしたり疑うことはたくさんあるな。。
典型的な脆弱性は覚えて置いて損はなさそう

フォレンジック

フォレンジックはpcapのログからflagを探したりファイルを復元してflagを入手したりする。CTFにおいてはフォレンジックの問題が解いてて一番楽しい。

pcapのログを見るのに必要なWiresharkの機能の使い方やデータの抽出方法の解説があった。バイナリについては与えられたファイルの拡張子が何であるか確認するfileコマンドや解析に便利なstrings,binwalkコマンドなどの説明があった。icatコマンドは知らなかったのでありがてえ
CSAWCTF2017のフォレンジックの問題でpcapの通信ログに謎のURLパラメータが大量にあるものがあった。その時は解けなかったがWriteupでは最初のパラメータにBMPの拡張子であるマジックナンバーが記述されていたらしく、パラメータを連結してBMPファイルを構築してflagを得るというものだった。
マジックナンバーは暗記しよう( ；∀；)

リバースエンジニアリング

実行可能なバイナリファイルの解析をする。アセンブリ言語を読めないと話にならないので、汎用、特殊レジスタの説明や代入や算術命令の説明があった。
callやjmp命令においてのスタックの構造把握が難しい。

講義が終わったあとはオリエンテーションというか1時間半くらいの問題を解く競争があった。結果は100人弱の中で27位だった。
時間が経つにつれて脳が停止してしまい、まともな思考ができなかった。終わった後すぐに別の200点問題の解き方がわかって悔しかった。。。
Writeupの解説を聞いて、自動で計算を処理して結果をPOSTするスクリプトを書く能力もいるのとバイナリ問題については処理の流れをしっかり掴むように読むことが大事なんだと思った。
Web問から行かずに、時間が経ってから正解者が多いWeb問を把握してそれから解いていく戦法使っている人がいて賢い。。。

まとめ

どの講義も全くの初心者の自分でもわかりやすい講義で最高だった。
リバースエンジニアリングについては他より覚えることが多い気がするので大変なのに1時間ちょっとで覚えるべきことだけ教えるといったスライドを作るのはめっちゃすごいと思った。
かっこいい~~原価割れした~~ステッカーも貰えるし、プロの人に懇親会で話を聞けるのでおすすめです。

まだ機械学習のするべき勉強は沢山あるけど、CTFの問題を解くのはすごく楽しいのでこっちもぼちぼちやってきたい。

隣の席で話しかけてくれた美人の女性さんと運営の皆さん、ありがとうございました。